1. Definition of AI
AI (Artificial Intelligence) is part of computer principle to simulate the human behavior intelligently.
AI란 사람의 행동을 지능적으로 모방하는 컴퓨터 이론의 일부분이다 (인지, 추론, 행동할 수 있도록 하는 컴퓨팅에 관련된 기술)
1-A. Strong and weak AI and example applications
- Strong AI? (General AI, 강 인공지능, 인간을 완벽하게 모방한 인공지능)
사람과 같은 지능
마음을 가지고 사람처럼 느끼면서 지능적으로 행동하는 기계 (지각력 - 독립성을 가짐)
추론, 문제해결, 판단, 계획, 의사소통, 자아 의식, 감정, 지혜, 양심을 갖음
모방 뿐만 아니라 그들 고유의 방식으로 지능이 존재한다.
ex) 인공 일반 지능, 인공 의식, 자비스
- Weak AI? (약 인공지능, 유용한 도구로써 설계된 인공지능)
특정 문제를 해결하는 지능적 행동
사람의 지능적 행동을 흉내 낼 수 있는 수준
대부분의 인공지능의 접근 방향 (현재 모든 AI는 약 인공지능이다.)
중국인 방 사고실험 (중국어를 몰라도 글자 모양에 따른 단어 조합 메뉴얼을 참조하여 답변)
약 인공지능은 지능을 모방할 수 있지만 반드시 mind나 menta states 나 consciousness를 가질 필요는 없다.
ex) 알파고
초인공지능?
강인공지능에서 발전하여 인간보다 월등히 뛰어넘는 인공지능을 초인공지능이라고 한다
ex) 비전
1-B. Symbolic and subsymbolic AI
- Symbolic AI
지식과 자료구조로 표현되어 지능을 프로그래머가 이해할 수 있도록 설계된 AI
게임, 정리 증명으로 부터 기원되었으며 심볼과 이산적인 변수들로 구성된다.
예시 : 명시적인 심볼릭 프로그래밍, 추론과 탐색, AI 프로그래밍 언어, 규칙, 온톨로지, 계획, 목표
장점
- 코딩하기 쉽다
- 디버그, 설명, 컨트롤하기 편하다
- 데이터가 크지 않다
- 사람의 사고로 설명하기 유용하다
- 추상적인 문제에 더 좋다
- Subsymbolic AI
신경망과 비슷한 레벨로 설계된 지능
예시 : 베이시안 학습, 딥러닝, connectionism
장점
- 노이즈에 대해 더 강직하다
- 더 퍼포먼스가 좋다
- 사전 지식의 요구가 적다
- 빅데이터로 크기를 키우기 쉽다
- 신경과학을 적용시키기 더 유용하다
- 지각 문제에 더 좋다
2. Knowledge Representation and Inference Systems
AI의 메인토픽은 sensing, thinking, acting으로 나뉘는데 Knowledge Representation 및 학습은 thinking과정에 해당한다.

2-A. Knowledge Representation (지식표현)
지식?
경험이나 교육을 통해 얻어진 전문적인 이해와 체계화된 문제 해결 능력
- 암묵지 (형식으로 표현하기 어려움, 학습 + 경험을 통함)
- 형식지 (형식으로 쉽게 표현됨)
- 절차적 지식(절차)
- 선언적 지식(성질, 특성이나 관계 서술)
지식 표현
두가지 카테고리로 나눌 수 있다
- 기호 기반(규칙, 프로엠, 의미망[flowchart], 논리 등)
문제해결에 이용하거나 심층적 추론을 할 수 있도록 지식을 효과적으로 표현하는 방법 (IF,THEN 규칙, 프레임, 의미망, 논리[명제논리, 술어논리], 스크립트 등)
- 함수 기반 (신경망, SVM, 회귀 등)
기호 대신 수치값과 수치값을 계산하는 함수를 사용하여 지식을 표현한다.
각 카테고리에 속한 지식 표현
- 규칙 : IF(조건) / THEN(결론)으로 규칙을 표현
인과관계, 추천, 지시를 전략(일련의 규칙) / 휴리스틱(경험적 지식) 으로 표현할 수 있다.
- 프레임 : Slot의 집합으로 지식 표현
- 논리 : 명제와 논리식을 사용하여 문장을 표현 (논리식 테이블(진리표)도 참고)
- 논리식? : 리터럴, 절, 논리곱 정규형, 논리합 정규형, 정형식(논리에서 문법에 맞는 논리식)
타당한 논리식(항진식) : 모든 모델에 대하여 항상 참인 논리식
항위식 : 모든 가능한 모델에 대해서 항상 거짓이 되는 논리식
충족가능한 논리식 : 참으로 만들 수 있는 모델이 하나라도 있는 논리식
충족불가능한 논리식 == 항위식
동치관계 : 어떠한 모델에 대해서도 같은 값을 갖는 두 논리식 (이를 논리식을 변환할 수 있다.)
논리적 귀결 : wff(well-formed formula)의 집합

명제 논리 : 문장으로 표현된 지식으로 부터 기본 명제들을 추출
술어 논리 : 명제의 내용을 다루기 위해 변수, 함수들을 도입하고 이를 술어를 통해 나타남, 존재 한정사와 전칭 한정사를 통해 표현됨
2-B. Inference (추론)
가정이나 전제로부터 결론을 이끌어 내는 것
규칙기반 시스템의 추론(전향 추론 / 후향 추론), 확률 모델의 추런 (관심 대상의 확률 또는 확률분포를 결정 / 베이즈 정리 및 주변화 이용)
귀납적 추론(규칙), 연역적 추론(명제로 부터 새 명제)
학습 또는 탐색(최적 정답 경우의 수에서 탐색)이 있다.
3. Uncertainty representations (불확실성의 표현)
3-A. 불확실성의 원인 (원인 -> 표현 방법)
- 약한 관련성과 지식 : 약한 인과성과 애매한 연관관계인 지식표현 -> 확신도 사용 표현 / 베이즈 정리 사용 표현
- 부정확한 언어 사용 : 자연어는 본질적으로 모호하고 부정확함 -> 퍼지이론 사용 표현
- 불완전하거나 결손된 데이터 기반 지식 -> 알려지지 않는것으로 간주하고 근사적인 추론 진행
- 상충되는 지식의 통합
확신도? (certainty factor) : 규칙과 사실의 신뢰정도를 [-1, 1] 구간의 값으로 표현
확률? : 어떤 사건이 일어날 가능성, [0,1] 구간의 값으로 표현
Sensitivty(민감도) and Specificity(특이도)

Sensitivity(민감도) : A와 B의 공통된 양성 / A에 대해 판단한 모든 양성 (진양성 / 진양성 + 위음성)
Specificity(특이도) : A와 B의 공통된 음성 / A에 대해 판단한 모든 음성 (진음성 / 진음성 + 위양성)
3-B. Bayesian theorem and inference
베이즈 정리 : 사건 A가 발생했을 때 사건 B가 발생할 조건부 확률


베이즈 정리를 활용한 베이즈 추론
모든 규칙을 IF THEN으로 표현하고, 확률을 계산한다.
결합 확률, 사건 A와 B가 동시에 일어날 확률
예시 ) P(A) = 0.1%, P(B|A) = 99%, , P(ㄱB | ㄱA) = 98% -> 질병에 걸렸다고 검진받았을 때 진짜로 걸렸을 확률은? (P(A|B)는?)

놀랍게도 0.047정도로 4%에 지나지 않는다. 발병률이 매우 적은게 그 이유인듯 하다.
이를 단일 가설에서 다중 가설로, 단일 증거에서 다중 증거로 확장한다면?

각 증거 가 서로 조건부 독립성을 띈다면 다음과 같이 확장시킬 수 있다
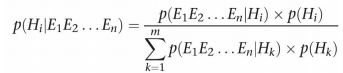
위를 확장시켜서 각 가설과 각 증거에 대해 표현하면 다음과 같다
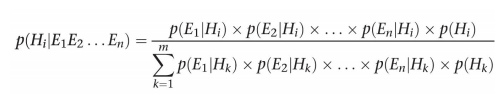
(다시 직접 정리해보자.)
이를 활용하여전문가 시스템은 어떻게 각 가설에 대해서 사후 확률을 계산하고 순위를 매길 수 있을까?

이렇게 보았을 때 3번째 가설이 더 효과적이다.
LS와 LN에 대한 것
LS : Likelihood of Sufficiency (충분 가능성), 증거 E가 있을 때 가설 H를 신뢰하는 정도
LN : Likelihood of Necessity (필요 가능성), 증거 E가 없을 때 가설 H에 대한 불신의 정도

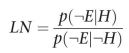
두가지는 서로를 유도할 수 없다. Why? 사후확률일 뿐이니까!, 전체 확률은 1-P(H)이지만 사후확률은 그렇게 유도가 안되니까!!
LS와 LN값을 제공하기 위해 전문가가 정확한 조건부 확률 값을 결정할 필요는 없다. 전문가는 그 가능성을 결정하기만 하면 된다.
LS값이 크다는 말은 증거가 관찰되면 그 규칙이 가설을 강력하게 뒷받침하며, LN이 작다는 말은 증거가 없다면 그 규칙이 가설을 강력하게 반대한다는 의미이다.
규칙기반 전문가 시스템에서는 사전 확률 P(H)를 사전 가능성(Prior odds)로 변환할 수 있다.


이를 통해 사전 가능성과 사후 가능을 나타낼 수 있다. 여기서 사후 가능성은 사후 확률을 구할 때 쓰인다.

이렇게 사전 가능을 통해 만든 사후 확률을 구하는 과정과 실제 사후확률의 차이를 비교해보자.

3-D. 베이즈 추론 VS 확신도
베이즈 접근과 확신도는 서로 다르지만, 개인적이고 주관적이며 질이 좋은 정보의 양을 잴 수 있는 전문가를 찾아야 한다는 공통점이 있다. (전문가를 찾는 이유는 불확실성에 대해 편협해지지 않기 위함)
베이즈 방법은 신뢰성 있는 통계 데이터와 진행을 이끌어갈 지식 공학자가 있고, 결정에 대해 전문가와 분석적이고 진지한 대화를 할 수 있는 경우에 가장 적합하다. (그렇지 않다면 유의미한 결과를 내기 어렵다)
베이즈 신뢰 전파는 지수적으로 복잡하여 큰 지식 기반에는 실용적이지 않다.
확신도 기법은 비록 이론적인 기반이 부족하지만, 전문가 시스템에서 불확실성을 다룰 수 있는 단순한 접근 방식을 제공하고, 여러 응용 분야에서 인정할 만한 결과를 제시한다.
3-F. 규칙기반 전문가 시스템의 불확실성 다루기 요약
불확실성은 믿을만한 결론을 위한 정확한 정보가 부족함을 뜻한다. 전문가 시스템에서 지식이 불확실해지는 이유는 상관관계가 취약한 함축, 부정확한 언어, 데이터의 분실, 다른 전문가의 관점을 통합하면서 겪는 어려움 때문이다.
베이즈 규칙
확률 이론은 전문가 시스템에서 불확실성을 다룰 수 있도록 정확하고 수학적으로 올바른 접근법을 제시해준다. (prospector는 이를 적용한 첫 시스템)
베이즈 접근법에서 가설 H의 사전 확률과 증거 E가 있는 경우, 신뢰도를 측정 시 충분 가능성 LS값을, 증거가 없는 경우 가설에 대한 불신도를 측정 시 필요 가능성 LN 값을 제공해야 한다.
베이즈 접근법을 적용 시 증거의 조건부 독립성, 믿을 만한 통계 데이터, 각 가설에 대한 사전 확률이 필요하다.
확신도 이론
확신도 이론은 전문가 시스템에서 불확실성을 다루는 판단적 접근 방식을 제공한다. 전문가는 증거 E를 관찰했을 때 가설H에 대한 신뢰 수준을 표현하기 위해 확신도 cf를 제공해야한다.
확신도는 확률이 알려지지 않았거나 확률 값을 쉽게 얻을 수 없는 경우에 사용한다. 확신도 이론은 신뢰 정도가 서로 다른 증거뿐만 아니라 점진적으로 습득하는 증거, 가설의 논리적 결합을 다룰 수 있다.
4. Probabilistic Graphical Models (확률 그래피컬 모델)
4-A. 확률 그래피컬 모델
확률 그래피컬 모델 : 확률변수로 정의하고 이들의 상호작용을 그래프로 표현하여 그래프에서 확률 추론을 수행
확률 이론 + 그래프 이론, 이를 통해 확률분포를 표현하고 확률변수에 대한 확률을 계산할 수 있는 모델
그래프 표현 : 인과관계를 Edge로 표현하여 그래프를 만들고 확률을 부여하여 확률 그래피컬 모델이 됨

베이지안 네트워크는 인과관계를 나타내기 위해 방향 Edge를,
마르코프 랜덤필드는 인과관계가 없는 문제를 다루므로 무방향 Edge를,
DBN은 RBM을 여러 층으로 쌓아 만들어진다.
결합 확률 : 결합확률을 모두 알아내긴 차원의 저주때문에 어렵다.
그래프 분해 : 직접 상호작용하는 확률변수만 Edge로 연결한다. 결합확률을 알아낼 필요가 없어지고 분해된 그래프에서 부분집합의 확률분포만 알아내면 된다. (연결이 없다면 중간 노드를 통해 상호작용이 됨)
4-B. 베이지안 네트워크?
마르코프 랜덤필드나 DBN보다 더 엄격한 확률모델
확률변수 사이의 인과관계를 조건부 확률로 표현하므로 불완전 데이터를 처리할 수 있다
데이터와 전문가 지식을 혼용해 사용할 수 있다.
베이지안 네트워크의 문제
- 1. 구조학습 (그래프 구조만들기)
확률 변수는 사람이 결정해야함. 인과관계는 사람이 직접 지정 or 데이터로부터 자동으로 알아낼 수 있다.
- 2. 확률학습 (노드간에 확률을 부여하기)
루트노드의 사전 확률 and 조건부 확률 구하기
- 3. 확률 추론
앞선 작업 이후에 할 작업, 추론 과정


이와 같이 알려지지 않은 확률에 대해 추론할 수 있다.
단일 노드간의 확률을 구하기 뿐만 아니라 가장 다중 노드간의 확률을 구할 수 있다.

직접 풀어보자면 P(A and B) = P (A and B and C) + P (A and B and !C)이고 각 식을 하나씩 풀어보면 P(A and B and C) = P(A | B and C) * P(B and C)와 같이 전개할 수 있고, P(B and C)는 또 P(B|C) *P(C)로 전개할 수 있다.

이를 일반화 한다면 다음과같다.

마르코프 조건
이와 같이 결합확률을 최소의 횟수로 분해하기 위해서는 그래프가 분해되어야 한다.
이때 그래프 분해에 필요한 조건은 마르코프 조건이다.

즉, 직접적으로 연관관계가 있는 노드만 남기자는 것이다.
예를 들어 엑스레이의 경우에는 페암에게만 영향을 받기 때문에 이외에는 모두 지운것을 확인할 수 있다. 물론 폐암은 흡연과 기타 노드들의 영향을 받기 때문에 축약 이전과 같은 정보를 내포하고 있다.
5. D-분리
조건부 독립을 찾기 위한 조건들
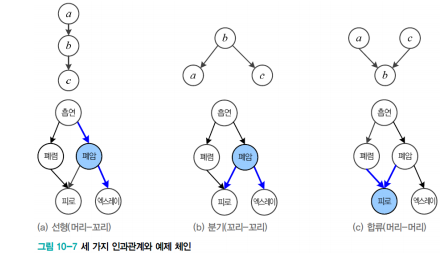
선형의 경우, 중간 노드를 알 때 흡연과 엑스레이가 독립이 되고, I(엑스레이, 흡연 | 폐암)
분기의 경우, 중간 노드를 알 때 피로와 엑스레이가 독립이 되고, I(엑스레이, 피로 | 폐암)
합류의 경우, 중간 도르를 모를 때 폐렴과 폐암이 독립이 된다, 대신 피로를 알게 되면 2개의 노드가 서로에게 영향을 주므로 독립이 아님이 설명된다. (피로가 결정되었고 폐암이 결정되었다면 폐렴이 아닐것인것 처럼)
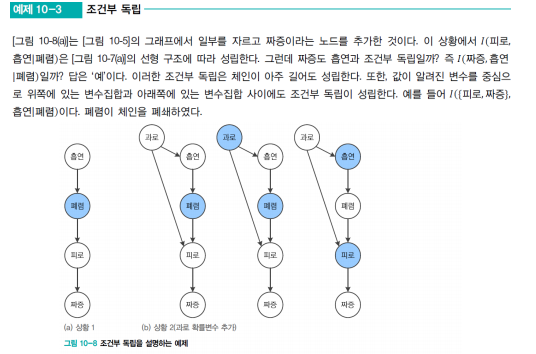

이와 체인이 폐쇄되고 열리게 된다.
이를 확장시키면 다음과 같은 큰 체인에 대해서도 독립, 분리에 대해 설명이 가능하다.


이 독립을 통해서 무엇을 알 수 있는가?
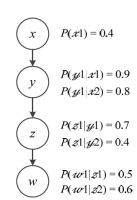
P( w_1 | x_1 )을 구한다고 하였을 때 x를 바로 구할 수 없음에도 y와 z를 거쳐서 계산이 가능하다.
즉, d-분리로 정의된 독립을 통해 베이지안 네트워크에서 계산량을 획기적으로 줄일 수 있다.

와 같이!
6. Markov random field (MRF)
이전까지 했던 것은 이웃한 노드 사이에만 직접적인 상호작용을 표현하는 베이지안 네트워크였다
이제 노드 사이에 인과관계가 없는 무방향 그래프를 사용하여 확률 변수가 동일한 자격으로 영향을 주고받으며 필드를 형성하는 마르코프 랜덤필드를 배워보자
마르코프 랜덤필드의 그래프 분해 방식
클릭을 이용하여 분해
클릭은 완전 부분 그래프, 극대 클릭은 노드를 추가하면 더 이상 완전 그래프를 유지하지 못하는 클릭

6-A. 깁스 확률분포?

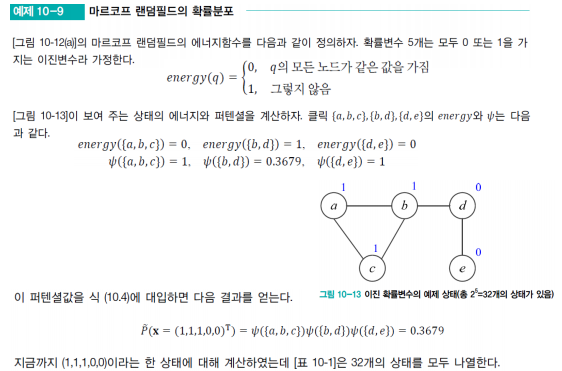
우선 클릭을 이용하여 그래프를 분배하는 것이고 문제에 맞는 에너지 함수를 알아서 정해야 한다. 이를 통해 퍼텐셜 함수를 정의하고 퍼텐셜로 정의되는 확률분포를 참조하면 확률을 구할 수 있다.
이곳에 경우 에너지 함수를 모두 같은 노드인가, 아닌가를 통해 값을 도출하는 함수이고, 이를 통해 퍼텐셜 함수가 정의된 후, 이를 통해 확률분포를 참조하여 확률을 구한다.

7. Informed and uninformed Search Methods
7-A. Uninformed search
문제에 대한 정보를 사용하지 않는 탐색
- Depth-first search (DFS)
무한 깊이에 빠지거나 루프에 빠질 수 있으므로 완전하지 않다.
최적이지 않다
- Depth-limited search (DLS)
완전하지 않고 최적이지 않다.
- Iterative deepening search (IDS)
정답이 있는 깊이가 유한하다면 완전하고
최적이다. (위치는 다를 순 있어도 깊이는 같을 것이므로)
- Breadth-first search (BFS)
완전하다
최적의 목표가 목표 중 가장 얕은 깊이에 존재한다면(즉, 간선의 비용이 non-decreasing function이라면) 최적이다.
DFS보다 공간복잡도 보다 더 크다.
- Uniform-cost search (UCS)
경로의 총 코스트가 가장 값이 작은 node를 방문한다. 만약에 각 Edge의 값이 1이라면 BFS와 같다.


"cost >= 엡실론" (엡실론은 최소 Edge크기, 양수여야만 완전하다.)
만약에 엡실론 0이고 이후에 루프가 생기면 완전하지 않다
최적이다.
7-B. Informed search
문제에 대한 정보를 활용하여 탐색하는 방법.
- Heuristics
얼마나 목표에 가까운지 평가하는 함수.
이 함수의 예로는 맨하튼 거리, 유클리디안 거리 등이 있다.
- Greedy search
위의 휴리스틱 함수를 이용하여 탐색에 활용하는 것이 Greedy search이다.
- A* search
그리디는 완전하지만 최적이진 않았다.

그 이유는 휴리스틱 함수가 올바르게 정의되어 있지 않을 수 있기 때문이다. 그렇기 A*는 휴리스틱 함수에 특정 조건이 추가된 Admissible heuristics이어야 하는 것이다.

여기서 h*(n)은 목표까지의 실제 cost이다.
이렇게 휴리스틱이 admissible하다면 최적일것이다.
이것에 대한 정의는 다음과 같다.
A가 정답이고 B가 sub-optimal이고 n이 정답A에 포함되는 노드 중 가장 가까운 방문된 노드라고 할 때 sub-optimal인 B보다 A가 먼저 방문됨을 증명하면 된다.

1. f(x)이 f(A)보다 작거나 같다. -> f(n) = g(n) + h(n)이고, Admissible heuristic의 정의에 의하여 f(n) <= g(A)이므로!
2. f(A)가 f(B)보다 작다 -> sub-optimal과 optimal의 정의에 의해 g(A) < g(B)일것이고, 휴리스틱의 정의에 의해 골에서의 휴리스틱 값은 0이므로 f(A) < f(B)이다.
3. 1번과 2번에 의해 f(n) <= f(A) < f(B)이므로, n을 먼저 방문하고, 정답 A안의 경로 노드인 모든 n은 B보다 먼저 확장되므로 A가 B보다 먼저 방문될것이다.
따라서 A*는 최적이다.
무한의 f(n) <= f(G)인 노드가 존재하지 않는다면 완전할 것이다.
heuristic 함수가 admissible하다면 최적일 것이다.
Relaxed problem?
행동에 제약이 더 적은 문제이다.
relaxed problem의 최적의 해답은 원 문제의 admissible heuristic이다.
왜냐하면 원 문제의 해답이 Relaxed problem의 해답이기도 하기 때문이다.
- Simple Memory Bounded A* search (MBA*)
A*와 같지만, 메모리가 꽉 차면 최악의 노드(즉, f(n)의 값이 가장 큰 노드)를 삭제한다. (만약 값이 같으면 가장 오래된 노드를 삭제)
최적의 해답을 찾을 수 있다.
만약 메모리에 root부터 최적의 해답을 저장할 수 없다면 정답에 다다르지 못한다.
최적의 얕은 해답을 저장할 수 있다면 완전하다.
지금까지의 알고리즘 중 최고
Admissible Heuristic을 만드려면?
Admissible Heuristic의 해답은 relaxed problem의 해답과 같다.
Admissible Heuristic이 더 실제와 같다면 정답에 빠르게 다가갈 수 있따.
Graph에선 Admissible뿐만 아니라 Consistent해야한다
Consistent하다는 것은?

7-C. 요약

8. Game Search
8-A. Mini-max search algorithm and its properties
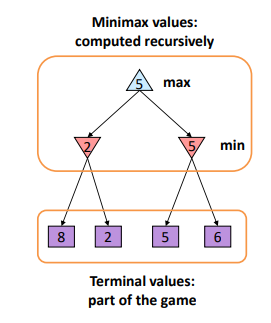
나는 MAX, 상대는 MIN
기본적으로 게임 트리의 완벽 Depth-first exploration이다. 때문에 Time과 Space가 DFS와 같다.
완전한가? : 트리가 유한하다면 Yes
최적인가? : Yes
기본적인 움직임이 DFS와 같은것이지 모든 노드를 다 돌기 때문에(즉, Complete DFS이므로) complete하고 optimal하다.
8–B 𝛼 − 𝛽 pruning
𝛼는 max중에서 가장 선택 값이 높은 값(-inf로 초기화), 𝛽는 min 중에서도 가장 선택 값이 낮은 값(inf로 초기화)이다.
재귀적으로 호출되므로 범위를 좁혀 내려간다. 이렇게 선택된 𝛼와 𝛽를 기준으로 가지치기를 한다.
이런 가지치기는 최종 결과에 전혀 영향을 미치지 않고, 최선의 케이스는 최선으로 선택되어, 절반의 노드만 탐색하므로 O(b^(m/2))이다.
들어간 값과 𝛼를 비교하고 크면 𝛽에 넣고 작거나 같으면 가지친다.
들어간 값과 𝛽를 비교하고 작으면 𝛼에 넣고 크거나 같으면 가지친다.

다음과 같은 흐름을 갖는다.
homepage.ufp.pt/jtorres/ensino/ia/alfabeta.html
Minimax game search algorithm with alpha-beta pruning
homepage.ufp.pt
데모 사이트이니 한번 직접 돌려보자.
이에 대한 평가는 다음과 같이 나타낼 수 있다. f(x)는 문제마다 정의되야 하지만 결국에는 weight가 곱해진 features의 합이다.

9. Local Search Methods
트리 탐색은 방문하지 않은 노드를 탐색한다. 그리고 정답까지의 경로 그 자체는 정답과 상관이 없다.
이러한 경우에는 Local search 알고리즘을 사용한다.
Local search란? : 더 나아질 곳이 없을 때 까지 단 하나의 옵션을 향상시킨다.
9–A. Hill-climbing search
현재 상태를 유지하고, 향상시키고자 한다. (이웃만 움직임)
-> 아무곳에서 시작하고, 가장 최선의 이웃으로 이동하는 것을 더 나아질 이웃이 없을 때 까지 반복한다.
하지만 이것은 local maximum에 빠지기 쉽다.

이러한 Local search Algorithm의 Optimization은 두가지로 나눌 수 있다.
9-B. 최적화 함수
1. Function Optimization (continuous optimization, 예시 : gradient descent)
객체 함수 : function evaluation
함수를 최대화 하는 변수를 찾는것

2.Combinatiorial Optimization (discrete optimization, 예시 : Genetic algorithm for TSP)
객체 함수 : path length
제한 범위를 이용한 함수를 최적화 하는 것

9–C. Gradient descent method (continuous)
위에서 알아본 Gradient descent에 대해서 알아보자.
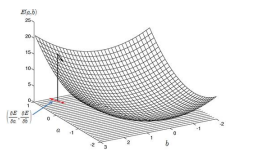
미분으로 얻은 경사의 반대방향으로 계속 움직이다보면 더 나아질 곳이 없는 위치(최적)를 얻을 수 있을것이다. (즉 현재 위치 - e[learning rate] * f'(x))
9-D. Hill-climbing search VS Gradient descent method (continuous)
Gradient descent?
경사 주변의 이웃을 보고 가장 가파른 위치로 이동한다.
연속적인 함수를 최적화하고 기울기를 계산한다.
Hill-climbing
모든 이웃들의 상태를 보고 각각의 cost function을 평가한다.
종종 discrete states의 문제를 최적화 하기 위해 사용된다.
Gradient descent보다 덜 효과적이다.
9-F. Simulated Annealing Search (SA)
지역 최댓값으로 부터 탈출하기 위해서 의도적으로 좋지 않은 움직임을 허락한다. 이 빈도는 점점 더 뜸해질것이다.
빈도 : hill-climbing은 절대 안좋은 값으로 안간다. 지역 최대로부터 탈출하기 힘들기 때문에 hill-climbing에 random walk를 더해 구현된다.

차이값이 클 수록, T값이 낮을수록 random하게 움직일 확률이 낮다 (주어진 대로 움직인다)
여기서 T는 숨겨진 값으로 0에 수렴하게 된다.
