문제

문제 분석
티어에 비해 꽤 까다로운 문제였다.
가장 문제라고 생각했던 것은 "치즈가 없는 칸, 0이 치즈 속의 빈 공간인가 혹은 바깥과 연결된 0인가"를 판별해야 한다는것을 생각해내고 구하는 부분이었던것 같다.
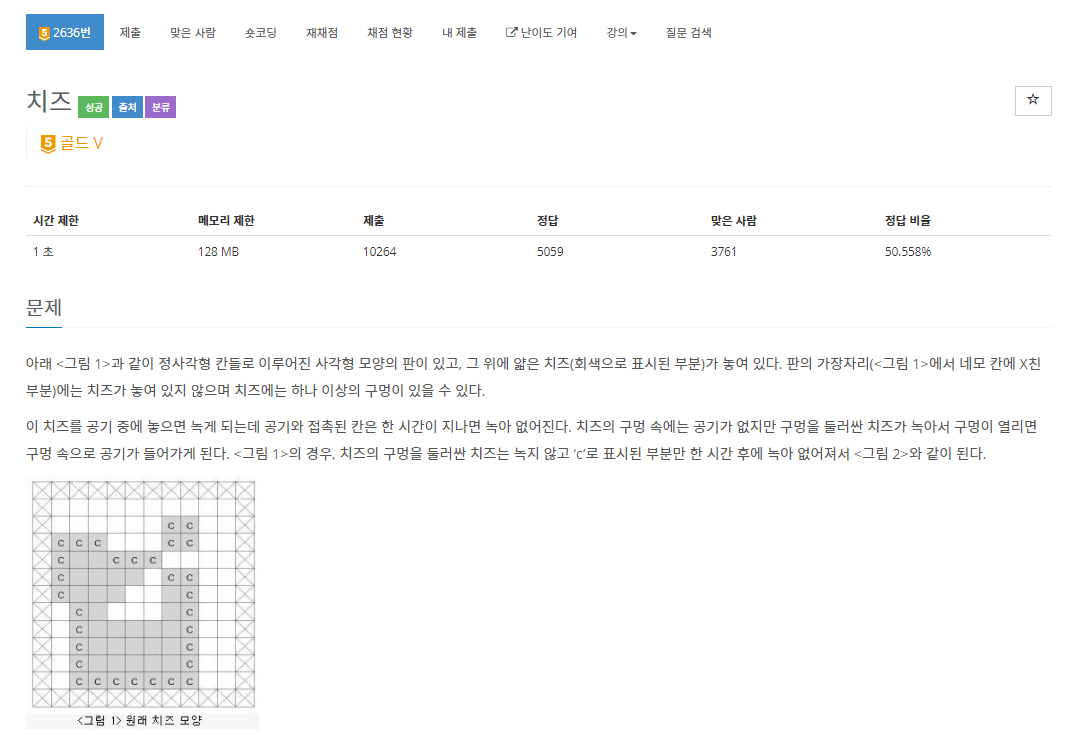
그림1과 그림2만 보더라도 같은 0이라도 그림1 근처의 빈 공간의 치즈들은 녹지 않는 반면 그림 2의 빈 공간은 바깥과 연결되어있는 빈칸이기 때문에 빈칸 옆의 치즈들도 녹게 된다.
그렇다면 이 빈 공간을 판단하는 방법은 무엇일까?
점 0,0에서 시작해서 0으로만 이동하는 BFS를 통해 구하면 결국 치즈 바깥만 0으로 남아있는 치즈 그림자가 생성될것이다.
그렇다면 바깥쪽 치즈는 무엇일까? 위 아래 양 옆 중 하나라도 바깥과 연결되어 있다면 그 치즈는 바깥쪽 치즈일 것이다.
이렇게 생성된 새로운 치즈 그림자를 다시 BFS를 돌려서 모든 치즈그림자 속 치즈를 돌면서 바깥과 연결된 부분을 판별하면 될것이다.
이것을 치즈그림자가 0이 될 때까지하면 모든 치즈가 녹는 시나리오가 완성되는 것이다.
출력을 위해 물론 횟수와 이전에 존재했던 치즈칸의 갯수는 저장해둬야 할것이다.
코드
// code#include<stdlib.h>
#include<iostream>
#include<string.h>
#include<string>
#include<vector>
#include<stack>
#include<queue> // priority_queue 포함
#include<set>
#include<unordered_set>
#include<map>
#include<unordered_map>
#include<algorithm>
#include<math.h>
#include<climits> // 자료형 limit포함
using namespace std;
typedef long long int lld;
typedef unsigned long long int uld;
typedef unsigned int ui;
const int MY_INT_MAX = 2000000000;
int input_map[101][101] = {0};
int cheese_number_map[101][101] = {0};
int visited_map[101][101] = {0};
int offset_line[8][2] = {{0,1}, {0,-1}, {1,1}, {1,0}, {1,-1}, {-1,1}, {-1,0}, {-1,-1}};
int offset[4][2] = {{0,1}, {0,-1}, {1,0}, {-1,0}};
int N,M;
void bfs_boundary(int param_i, int param_j)
{
int cheese_num = 1;
cheese_number_map[param_i][param_j] = cheese_num;
queue<pair<int,int>> q;
q.push(make_pair(param_i, param_j));
while(!q.empty())
{
int current_i = q.front().first;
int current_j = q.front().second;
q.pop();
for(int i=0; i<4; i++)
{
int next_i = current_i + offset[i][0];
int next_j = current_j + offset[i][1];
if(next_i >= 0 && next_i < N && next_j >=0 && next_j < M && input_map[next_i][next_j] == 0 && visited_map[next_i][next_j] == 0)
{
visited_map[next_i][next_j] = 1;
bfs_boundary(next_i, next_j);
}
}
}
}
void bfs(int param_i, int param_j)
{
int counter = 0;
for(int i=0; i<4; i++)
{
int next_i = param_i + offset[i][0];
int next_j = param_j + offset[i][1];
if(next_i >= 0 && next_i < N && next_j >=0 && next_j < M && cheese_number_map[next_i][next_j] == 1)
counter++;
}
if(counter >= 1)
cheese_number_map[param_i][param_j] = -1;
queue<pair<int,int>> q;
q.push(make_pair(param_i, param_j));
while(!q.empty())
{
int current_i = q.front().first;
int current_j = q.front().second;
q.pop();
for(int i=0; i<8; i++)
{
int next_i = current_i + offset_line[i][0];
int next_j = current_j + offset_line[i][1];
if(next_i >= 0 && next_i < N && next_j >=0 && next_j < M && cheese_number_map[next_i][next_j] == 0 && visited_map[next_i][next_j] == 0)
{
visited_map[next_i][next_j] = 1;
bfs(next_i, next_j);
}
}
}
}
void solution()
{
// code
cin >> N >> M;
for(int i=0; i<N; i++)
for(int j=0; j<M; j++)
cin >> input_map[i][j];
int output = 0;
int prev_count = -1;
while(1)
{
output++;
int tmp_count = 0;
for(int i=0; i<N; i++)
for(int j=0; j<M; j++)
cheese_number_map[i][j] = 0, visited_map[i][j] = 0;
bfs_boundary(0,0);
int flag = 0 ;
for(int i=0; i<N; i++)
for(int j=0; j<M; j++)
visited_map[i][j] = 0;
for(int i=0; i<N; i++)
{
for(int j=0; j<M; j++)
{
if(cheese_number_map[i][j] == 0 && visited_map[i][j] == 0)
{
visited_map[i][j] = 1;
bfs(i,j);
}
}
}
for(int i=0; i<N; i++)
for(int j=0; j<M; j++)
if(cheese_number_map[i][j] == -1)
{
input_map[i][j] = 0;
tmp_count++;
}
if(tmp_count != 0)
prev_count = tmp_count;
else
break;
}
cout << output-1 << endl;
cout << prev_count << endl;
}
int main ()
{
iostream::sync_with_stdio(0); // 이제 C stdio의 입출력 사용 불가
cin.tie(NULL);
cout.tie(NULL); // 개행도 \n로 하도록 하자.
solution();
return 0;
}물론 이 코드를 더 압축할 수도 있고 의미없는 부분을 지울 수 있겠지만 행여라도 잘못되면 어떨까 무섭다 ㅠ
개선점?
단순 input에 대하여 BFS, DFS를 돌린다는 생각보단
input을 연산하여 얻어진 데이터를 BFS, DFS돌리는 방안도 생각해보자.
이 문제에서 가장 골치아팠던 점은 현재 점에서 다음점으로 이동할 때 그 당시엔 내가 바깥이 될수도, 안될수도 있고 현재 점 뿐만 아니라 다음점에 대해서도 그 점이 바깥일지, 바깥이 아닐지 모른다는 부분이었다.
결국 모든 점을 다 돈 이후 다시 돌아와야만 그게 판결이 가능하다는 것이다.
그것을 체크해주기 위해서 그림자라는 새로운 배열을 만들어 저장했따.
'알고리즘' 카테고리의 다른 글
| 13270 백준 피보나치 치킨 (0) | 2021.03.15 |
|---|---|
| 백준 11054 번 가장 긴 바이토닉 부분 수열 (0) | 2021.03.14 |
| 6588, 15711 백준 (0) | 2021.03.10 |
| 2661 백준 (0) | 2021.03.06 |
| 15686 백준 (0) | 2021.03.06 |
