0. Gradient descent
이전에 Gradient descent가 어떤 의미를 갖는지 알아봤었다. 리마인드 해보자면, 다음과 같은 scores funcion이 있을 때

각 데이터 별로 실제 scores와 예측 scores를 이용하여 Loss(손실)를 계산하고, 모든 데이터에 대해 더했다.

이와 같이 하나의 스칼라로 나타나진 Loss라는 기준을 바탕으로, 이 값을 최소화 하는 방향으로 W를 업데이트 하기 위해서 우리는 Loss를 W에 대해서 미분한 값을 구하는 것이다.

이렇게 미분값을 구하고, W를 갱신하는 것을 iterative하게 함으로써 우리는 최적의 값으로 도달할 수 있다.

Gradient descent에서 가장 중요한 것은 어떻게 L을 w에 대해 미분한 값을 얻느냐 인데, 이 방식에는 직접 수학적으로 미분하여 값을 얻는 방식과, 분석적으로 미분값을 얻는 것이 있다.
직접 미분하는 경우에는 쉽게 쓸 수 있다는 장점이 있지만, 매우 느리고, 유사한 값이 도출된다는 단점이 있다.
분석을 통해 미분값을 얻는 경우에는 빠르고, 정확하다는 장점이 있지만, 오류에 취약하다는 단점이 있다. 또한, 이 식을 유도할 때 수학(특히 미분학)이 필요하고 수학적 검증이 필요하다는 주의점이 존재한다.
이번 포스팅에서는 주로 이 분석을 통해 미분값을 얻는 방식에 대해서 다루어 보겠다.
2. Gradient를 어떻게 얻을까?
2-1. Computational graph
미분값을 구하는 식에 앞서 어떻게 미분값을 유도하는 지에 대해서 알아보자. Computational graph로 우선 L을 나타내어야 한다. 다음은 Computational graph의 간략도이다.

Gradient descent의 식을 간단하게 그래프로써 표현한 것이다. 실제로는 매우 복잡하지만, 이 그래프는 직관을 위함을 인지하자.
이제 실제 식을 Computational graph로 나타내고, 이를 미분해보자. 다음과 같은 간단한 식이 있다고 해보자.
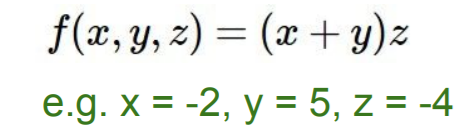
이를 Computational graph로 나타내면 다음과 같다.

여기서 우리는 최종 식 f에 대해 변수 x,y,z,에 대한 미분값을 알고자 하는 것이다.

예시로 든 식이 너무 쉽고, 그냥 미분하면 되는것 아니냐? 라는 의문이 들 수 있지만 실제 네트워크는 매우 복잡하므로 이는 사실상 불가능하다. 그렇기 때문에 대부분의 경우, 앞으로 서술할 Backpropagation(역전파)를 사용한다,
2-2. Backpropagation (역전파)
역전파의 키포인트는 Chain rule을 통한 순차적인 미분이다. 이 미분 과정을 간략히 보자면, 첫번째로 하나의 식을 여러개의 노드로 나눈다. 둘째로 정의한 intermediate node를 각 변수에 대해 미분하여 local gradient를 얻는다. 셋째로 chain rule을 이용하여 L에 대한 intermediate node의 미분값을 얻는다. 이 과정을 변수까지 역전파 해감으로써 우리는 원하는 미분 값을 얻을 수 있다.
예를 들어, 앞서 소개한 식을 이용하여 직접 미분을 해보자. 위 식에서 하나의 식을 다음과 같이 그룹화 할 수 있다.

앞서 정의한 intermediate node의 local gradient를 계산한다.

이제 chain rule을 이용하여 미분한다. af/af = 1이고 정의에 의해 af/az = q이다. 중요한 것은 그룹화 한 af/aq = z = -4인데, chain rule에 의해 af/ay = af/aq * aq/ay이므로 우리가 원하는 af/ay를 구할 수 있다.

이 과정이 매우 복잡해보일 수 있는데, 이를 하나의 노드에 대해 살펴보면 매우 직관적이다. 아래 일반화 된 노드를 살펴보자. 앞서 설명한 local gradient와 위에서 내려온 upstream gradient를 이용하여 L에 대한 Local variable의 미분값을 구하는 것을 도식화 한 것이다.

aL/az가 aL/aL부터 시작하여 역전파 되어 upstream gradient값이 도착함이 재귀법으로 자명하고, local gradient를 이용하여 intermediate node의 소속 노드들에 대한 미분값을 구할 수 있기 때문에 이를 반복하면 결국 우리가 구하고자 하는 L에 대한 파라미터의 미분값을 알 수 있음도 자명하다.
2-3. Node의 구성
지금까지 기본적인 연산 하나를 기점으로 computational graph의 노드를 구성하였고, 역전파 해보았다. 하지만 기본 연산 뿐만 아니라 미분이 가능하고 복잡하지 않다면 하나의 노드가 다중 연산을 표현하도록 구성할 수 있다. 다음 예시 식을 함께 보자.

이 식은 w0x0+w1x1+w2를 입력으로 하는 sigmoid function의 형태를 띄고 있다. sigmoid function가 미분 가능하고, 미분식이 명확하므로 이를 하나의 큰 노드로 다음과 같이 나타낼 수 있다.

하나의 단순 연산을 기준으로 노드를 나눌때와 결과가 같음을 확인할 수 있다.
2-4. Backward flow의 패턴
하나의 노드를 하나의 단순 연산으로 구성할 경우, local gradient가 단순해지므로, 역전파 시 나타나는 효과(패턴)이 명확하다. 각 연산별로 어떤 특징을 갖는지 그림을 보면서 확인해보자.
-1. 덧셈 : gradient 분배기

x+y와 같이 하나의 노드에 +연산만 속한다면, 그 노드의 local gradients는 1이므로 upstream gradient가 그대로 두 노드에 역전파된다.
-2. max : gradient 라우터

max연산의 경우에는 한쪽엔 그대로 x가, 한쪽엔 0이 들어가므로, local gradient의 값은 1 혹은 0이다. 따라서 한쪽에는 upstream gradient가 그대로 들어가고, 한쪽엔 0이 들어가는 gradient 라우터 역할을 한다.
-3. 곱셈 : gradient 스위처

x*y와 같이 단순 연산에서 local gradient는 x로 미분할 때 y가, y로 미분할 때 x가 도출된다. upstream gradient와 상대의 값을 곱하게 되는 gradient 스위처 역할을 한다.
2-4. Multivariate chain rule
지금까지 하나의 변수가 하나의 식에만 속한 형태의 computational graph로만 예를 들었다. 하지만 실제 식은 서로 얽히며 매우 복잡하게 구성되어 있다. 그렇다면 이런 경우에서는 어떻게 미분이 될까? 정말 간단한 예시로 다음을 확인해보자. 하나의 연산 결과가 서로 다른 노드에 속해져 있는 경우, 즉 ("x"+y) + ("x"+z)와 같은 경우 말이다. 이를 computational graph로 나타내보면 다음과 같다.

그렇다면 upstream gradient가 2개인데, 그렇다면 이를 어떻게 해야할까? x의 변화는 x+y와 x+z 두 노드에 속하고 영향을 주고 받으므로 두 upstream gradient를 모두 이용해야할 것이다. 그렇기 때문에 두 upstream gradient를 모두 더해야한다. 이를 예시와 함께 미분과정을 살펴보자.
예를 들어 e = (a+b)*(b+1)이라는 식이 있다고 생각해보자. a=2, b=1이 입력으로써 주어지고, a+b와 b+1을 c와 d로 나타내고 c+d를 e라고 노드들을 정의된다 할 때 computational graph로 나타내면 다음과 같다.

b가 multivariate chain rule를 갖는 상황이다. 이 상황에서 ae/ab를 구하고자 한다. b가 1이 커진다고 할 때 e가 얼마나 변하는지를 보면 multivariate chain rule이 어떻게 적용되는지 직관적으로 볼 수 있다. b가 1이 커지면, b에 대한 미분값을 통해 알 수 있는 것과 같이 c와 d는 각각 1씩 커지게 된다. c가 1 커진다면 e는 c에 대한 미분값으로 알 수 있는 것과 같이 2가 커진다. d가 1 커진다면 e는 d에 대한 미분값으로 알 수 있는 것과 같이 3이 커진다. 결국 b가 1 커진다면 e는 5가 커지게 된다. 이와 같은 방식으로 multivariate chain rule이 적용된다. 이 규칙을 "경로를 통한 합계 규칙"이라고 한다.
// 추가로 왜 굳이 덧셈인지, 덧셈외에도 제곱, 로그 등 다양한 연산에 대해서도 이 덧셈이 올바르게 적용되는지 추가로 조사해봐야겠다.
2-5. Vectorized gradient descent
지금까지 스칼라값의 데이터에 대해 역전파 해보았다. 하지만 실제 학습과정에서는 백터를 이용하여 데이터가 전달되는 경우가 많기 때문에 이 경우에는 무엇이 다른지 알아보자. 가장 큰 차이점은 차원이다. 어떻게 다를까?

x,y,z가 벡터이므로, gradient도 스칼라가 아닌 다차원이 되어야 한다. 이 local gradient는 Jocobian matrix이다. Jocobian matrix란, z의 각 원소를 x의 각 원소로 미분한 matrix이다. 이 matrix는 다음과 같이 구성된다.

결과적으로 upstream gradient x local gradient해서 도출된 새로운 upstream gradient는 L의 x에 대해 미분한 Jocobian gradient일 것이다. 이때 matrix의 차원은 (input vector의 갯수 x output vector의 갯수)일 것이다. 실제 학습에서는 전체 minibatch에 대해 한번에 연산하므로 ((input vector의 갯수 x minibatch수) x (output vector의 갯수 x minibatch수))가 된다더라~
이렇게 모든 노드의 연산된 미분의 차원은 반드시 자신의 입력 차원가 같아야 함을 유의해야 한다.
// 좀 더 자세하게 알아보자. 실제 갖는 값이라던가 형태(대각행렬이라던데 왜?)
실제 어떻게 미분되는지 예를 들어 확인해보자.

위과 같은 식이 있을 때, 이를 calcuational graph로 나타내고 계산하면,

와 같다. L2에서 미분은 2q이므로, 이를 적용시키면,
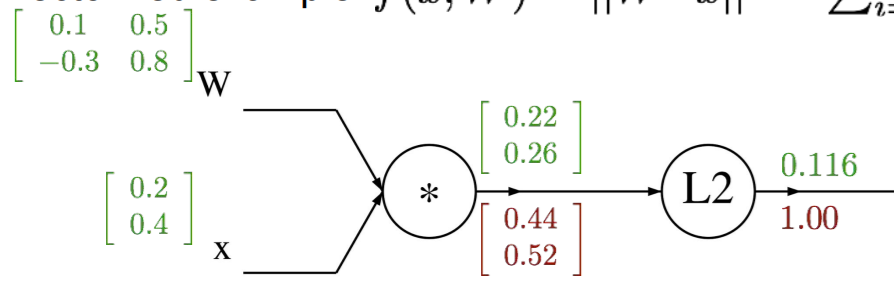
와 같다. q(k)를 W(i,j)에 대해 미분한다면, 벡터 미분에 의해서

이므로 upstream gradient와 연산하면, 다음과 같다.

이와 같이 x에 대해 q를 미분한 local gradient와 upstream gradient를 이용하여 f를 x로 미분한 결과를 도출할 수 있다.

// 벡터 미분이 매우 부족하다. 좀더 공부
2-6. 실제 구현
실제 구현에서는 각 노드가 어떻게 구현될까? 하나의 연산를 갖는 노드에는 결과 도출을 위한 forward와 gradient update를 위한 backward가 API로써 구현되어 있다. 간략한 구현을 확인해보자면, 입력을 통해 연산 결과를 리턴하는 forward 함수와, forward에서 cached된(저장된) 입력을 통해 표현된 local gradient와 인자로 전달된 upstream gradient를 연산하여 dx와 dy를 리턴하는 backward 함수가 있다.

이런 노드들이 단순 연산뿐만 아니라 sigmoid function과 같은 큰 노드에 대해서도 API에 정의되어 있고, 실제 네트워크가 forward / backward할 때 이를 호출하여 연산하는 것이다.

3. references
1. cs231n lecture4 : Backpropagation and Neural Networks
2. https://brunch.co.kr/@chris-song/22
계산 그래프로 역전파 이해하기
Backpropagation - 구글 브레인 Chris Olah | 이 글은 colah.github.io 의 블로그의 글을 저작자 Chris Olah의 허락을 받고 번역한 글입니다. http://colah.github.io/posts/2015-08-Backprop/ 서론 역전파(Backpropagation)는 딥 모
brunch.co.kr
'ML' 카테고리의 다른 글
| 인공 신경망 학습 (0) | 2021.07.05 |
|---|---|
| 합성곱 신경망 (0) | 2021.07.01 |
| ML-Agent 학습 환경 디자인 (0) | 2021.05.28 |
| 트리 탐색과 유전 알고리즘을 활용한 외판원 문제 근접해 구하기 (0) | 2021.05.12 |
| ML Agent의 강화학습을 활용한 Unity AI학습 (0) | 2021.05.11 |
