1. Fully connected layer vs Convolutional layer
1-1.Fully connected layer?
3차원 이미지를 1차원으로 펼쳐서 하나의 가중치 row에 대해서 모든 픽셀의 값을 내적(dot)한 값들의 집합으로 이미지 전체에 대해 학습한다.
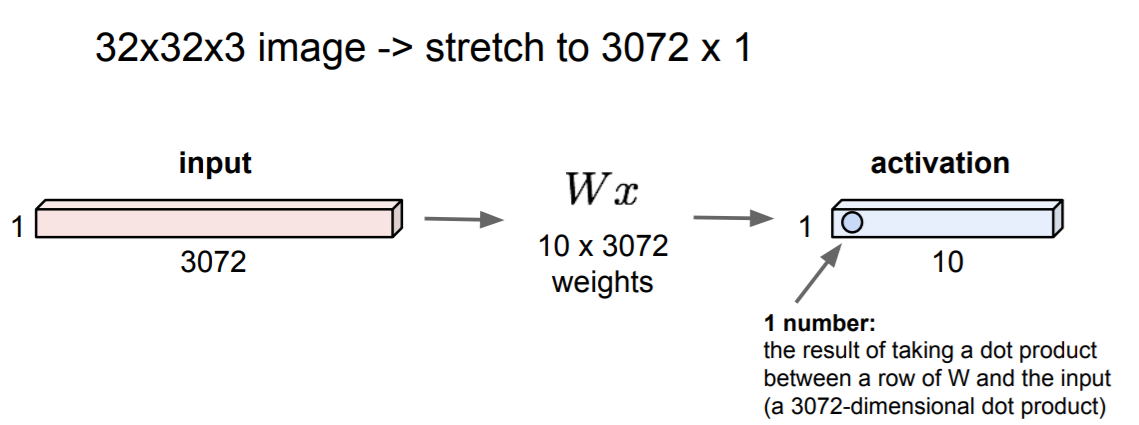
1-2. Convolutional layer
하나의 output이 이미지 전체가 아닌 일정 구역에 대한 내적값이기 때문에, fully connected layer와 다르게 이미지의 공간적 구조 및 정보를 유지하며 전파한다. (local connectivity)
3차원 필터가 3차원 이미지를 순회하면서(slide) 내적한다. 이때 필터의 깊이(depth)는 반드시 input의 depth와 같아야 한다. 이렇게 필터가 순회하면서 내적한 결과를 activation map이라고 한다. filter의 갯수는 다중이 될 수 있고, 이 갯수가 activation map의 depth가 된다.

하나의 activation map에서 동일한 좌표의 서로 다른 depth값들은 같은 spatial data에서 서로 다른 filter가 feature를 추출한 결과이다. 이와 같이 구성된 Convolutional layer와 활성화 함수, pooling 등이 겹겹이 쌓여 만드는 네트워크가 Convolutional network이다.
이 네트워크의 특징은 학습과정에서 따로 설정하지 않아도 역전파하여 가중치를 조정하면서 입력 계층에 가까운 layer일 수록 추출하는 feature는 edge 등과 같이 low-level feature이고, 출력 계층에 가까운 layer일 수록 추출하는 feature는 object등과 같이 high-level feature이 된다는 것이다. 이런 high-level feature를 linear separable classifier가 분류한다.
실제 Convolutional network의 feature map을 보면서 이를 확인해보자.

2. Convolutional layer에서 filter의 연산
하나의 layer에서 어떻게 input과 filter가 내적하여 결과값을 도출하는지 확인해보자.
예를 들어 7x7의 입력 데이터와 3x3 필터가 있다고 가정해보자. 문제의 단순화를 위해 depth는 고려하지 않는다

filter의 가중치와 filter의 위치에 해당하는 input의 내적값을 구한다. 이후, filter의 위치를 일정 칸(stride)을 이동한다. 이를 모든 이미지에 대하여 행하면 된다. 다음은 stride = 1일때의 다음 filter의 위치이다.
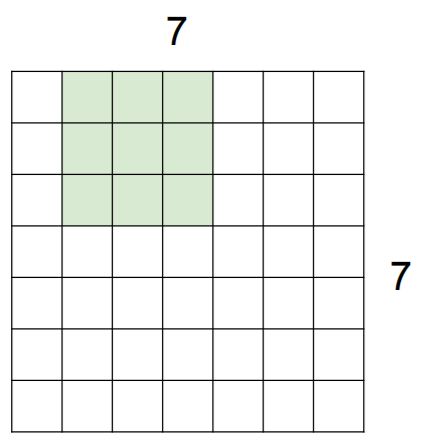
filter와 stride의 크기가 1이 아닌 이상, 필연적으로 output은 input의 크기와 달라질 수 밖에 없다. 또한, 이 크기에 따라 output을 도출하지 못할 수도 있다. 위의 예시에서 stride가 3이라면, 가장 오른쪽의 col값은 3, 6, 9가 된다, 하지만 이는 입력의 차원인 7을 넘는 값이므로, 불가능한 값이다. 이를 쉽게 먼저 확인하는 방식으로는 출력 차원을 예측해보는 방식이 있다. 출력의 차원 = ((입력 차원 - 필터의 차원) / stride ) + 1이므로, 이 수가 정수가 아니라면 불가능한 경우이다.
filter와 stride의 크기로 인한 또다른 문제로는 layer를 겹칠 수록 필연적으로 데이터의 차원이 작아진다는 것이다. 이렇게 되면 정보손실이 커지고, 코너에 대한 값을 잃게 되므로 이 문제를 해결하기 위해 입력의 주위를 0으로 채우는 padding을 활용한다.

이렇게 되면 원하는 대로 차원을 조정해 줄 수 있고, 정보 손실을 줄이고 코너에 대한 값을 유지할 수 있다.
// 질문 : 이렇게 하면 padding이 결과값에 영향을 주고, 가중치 갱신에도 영향을 줄것 같은데 이 영향이 전체 학습에 대해 악영향을 주는 것은 아닌가?
이제 한 layer에서 파라미터의 갯수를 계산해보자.
32x32x3이라는 입력에 대하여 stride가 1이고, padding이 2인 10개의 5x5크기의 필터가 있다고 한다면, 각 필터가 5x5x3 + 1(bias를 위해서) = 76개의 파라미터를 가지므로, 하나의 layer에는 총 76 * 10 = 760개의 파라미터를 갖는다.
실제로 이 하이퍼 파라미터들을 어떻게 초기화 시켜주는지는 다음 사진을 참고하자.

stride의 갯수가 커질수록 pooling과 유사하게 down sampling의 효과를 내어 파라미터의 갯수를 줄여주고 overfitting을 방지하는 등 영향을 줄 수 있다. 문제에 따라서 pooling보다 더 좋은 효과를 낼 때가 있다더라~
// 더 알아볼 것 : 언제 더 좋은 효과를 내는가? 무조건 효과가 좋으면 pooling을 절대 쓰지 않을텐데... 두 방식의 장단점은?
3. CONV layer의 API
이전에 역전파에서 배웠던 연산의 노드와 같이 딥 러닝 API에는 앞서 설명한 모든 값, 함수들이 정의되어 있다.

4. Pooling layer
데이터 형상을 작게하고, 관리될 수 있게 만들어준다. 즉, 파라미터의 수를 줄여주고 공간적인 불변성(Invariance over vision)을 획득하게 해준다. 이때 pooling의 연산은 각 activation map이 독립적으로 행해진다. 즉, 공간적으로만 pooling된다는 것이다. 서로 다른 filter는 같은 공간에 대해 서로 다른 feature를 뽑는것임을 다시한번 생각해보면 공간적으로만 pooling된다는 것이 명확할 것이다.

// 질문 : 공간적인 불변성 (Invariance over vision)은 어떤 의미지?
filter와 마찬가지로 pooling은 pooling의 차원과 stirde의 크기를 갖는다. 또한 pooling의 연산 종류도 다양한데, 예를 들어 pooling차원에 해당하는 공간에 대해 평균을 내는 연산과 최댓값을 뽑는 연산 등이 존재한다. 다음은 max pooling의 예시이다.

'ML' 카테고리의 다른 글
| 다양한 Gradient descent optimization (0) | 2021.07.05 |
|---|---|
| 인공 신경망 학습 (0) | 2021.07.05 |
| 역전파와 신경 네트워크 (0) | 2021.07.01 |
| ML-Agent 학습 환경 디자인 (0) | 2021.05.28 |
| 트리 탐색과 유전 알고리즘을 활용한 외판원 문제 근접해 구하기 (0) | 2021.05.12 |
