0. 더 나은 optimization
지금까지 사용했던 Gradient descent는 Stochastic Gradient Descent(SGD)였다. 하지만 실제로는 다양한 Gradient descent방식이 있으며 각 어떤 특징을 갖는지 확인해보자.
1. SGD의 문제점
우선 SGD의 문제가 무엇일까? 다음과 같은 상황을 가정해보자.

하나의 weight에 대한 Loss의 Gradient가 크고, 또 다른 하나의 weight에 대한 Loss의 Gradient가 작다면 즉, Hessian matrix에서 가장 큰 값과 가장 작은 값의 비율이 클 때, 다음과 같이 optimize한다.

이렇게 되면 Gradient가 작은 방향에 대해서는 optimize속도가 느리고, 큰 방향에 대해서는 변화가 요동친다. 이 문제는 차원이 높을 수록 매우 더 심해진다. 차원이 높을 수록 Hessian matrix의 크기는 커질 것이고, 값이 많아질 것이며 이에 따라 가장 큰 값과 가장 작은 값의 비율도 커질 것이다.
또 다른 문제로는 saddle point에 대한 처리이다. SGD는 단순 점에 대한 gradient를 구해야하므로, local optima에 빠지면 빠져 나올 수 없고, 거의 평평한 곳에서는 gradient가 0에 가까우므로 optimize속도가 매우 느려지게 된다.

또 다른 문제로는 이 gradient가 현재 위치에 대한 완벽한 gradient가 아닌, 미니배치에서 추정한 Loss이기 때문에 부정확하다. 그렇기 때문에 전체 데이터에 대해서 확인해보면 이 방식은 nosiy할 수 있다.

2. SGD + Momentum
그래서 이에 대한 문제점들을 해결하고자 속도의 개념을 포함시킨 SGD + Momentum방식이 나타났다. 이전 점까지 optimize한 방향이 현재 점에서도 유사한 값을 가질것이라는 개념이다. 다음은 두 방식에 대한 계산식의 차이이다.

일정한 비율의 이전 optimize 속도와 현재 gradient를 배합하여 새로운 optimize 속도를 얻는 것이다. 이때 비율은 0.9 혹은 0.99 등 다양한 수가 될 수 있다. 그렇다면 이렇게 이전 optimize 속도를 이용한 것과 기존 SGD의 optimize는 어떤 경향성의 차이를 가질까? 이전 SGD에서의 문제였던 Saddle point에서의 optimize와 Gradient Noise를 예로 확인해보자.
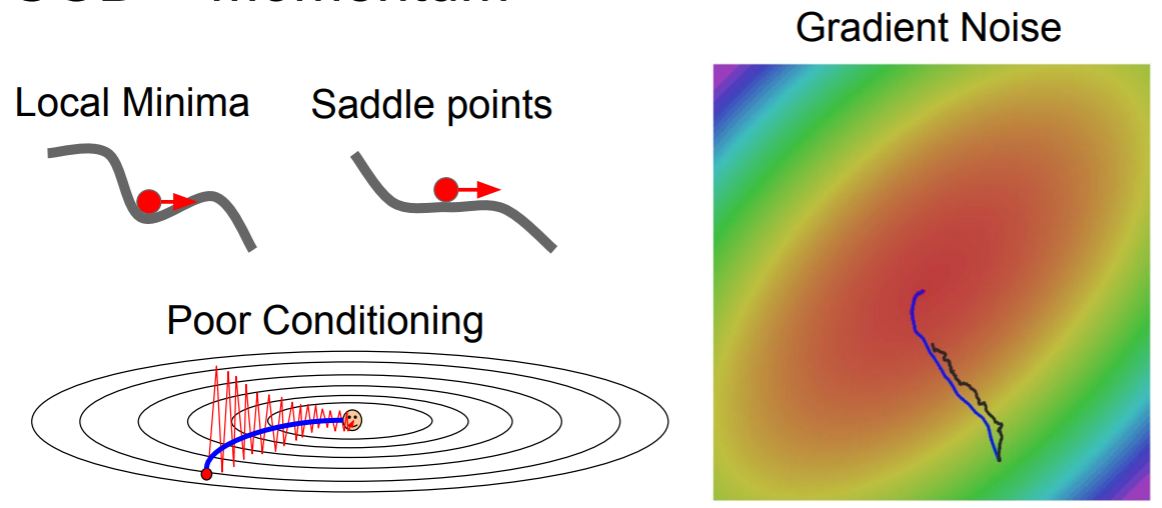
optimize 속도가 눈에 띄게 좋아졌고, 더이상 saddle points에서 멈추지 않으며 noise가 mometum을 더함으로써 평균화 되어 줄어들게 되었다. 하지만 이전 점의 optimize 속도를 일정량 이용하기 때문에 잘못된 optimize 방향으로 shoot over하는 문제가 있음을 인지할 수 있다. 이러한 문제를 최소화 하고자 Nestero Momentum 방법이 등장해다.
3. Nestero Momentum
Nestero Momentum은 이전 optimize의 속도와 "예측한 다음 점에서의 gradient"를 이용하는 것이다. 현재 점이 아닌 예측한 다음 점에서의 gradient를 이용한다는 점이 다르다. 이때 다음점 = 현재점 + 이전 점에서의 optimize 속도 로 러프하게 예측한다. 이 방식은 convex optimzation에선 잘 적용 될 순 있지만 neural network와 같은 non-convex한 모델에서는 사용할 수 없다더라. // 왜 안되는지는 더 공부해보고 알아보자.
이제 어떻게 구현될지와 어떤 optimize경향성을 보이는지 확인해보자.

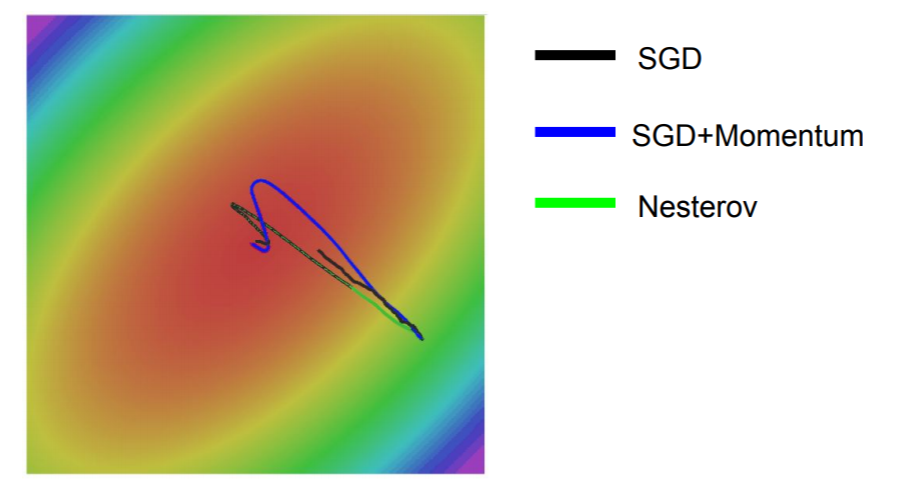
Nesterov는 이전 점에서의 optimize 속도를 이용하여 SGD보단 빠르고 덜 noisy하며, SGD + Momentum보다 덜 shoot over하는 경향성을 확인할 수 있다. (즉, Nestrov가 더 gradient에 민감한 경향이 있다) 그렇다면 이제 이런 의문이 들 수 있다. shoot over하는 경향성은 이전점의 optimize방향이 너무 큰 영향을 미치기 때문인데, 이를 이전 점이 아닌 전체에 대한 gradient를 이용하면 이 경향성이 줄어들지 않을까? 이것을 이용하는 것이 AdaGrad와 RMSProp이다.
4. AdaGrad
AdaGrad는 optimize과정에서 구한 gradient를 모두 제곱하여 더하고, 그 값과 현재점의 gradient를 이용하여 값을 update 하는 방식이다. Adaptive Gradient의 줄임말으로, momentum과는 다르게 gradient의 제곱을 축척한 값을 유지한다.
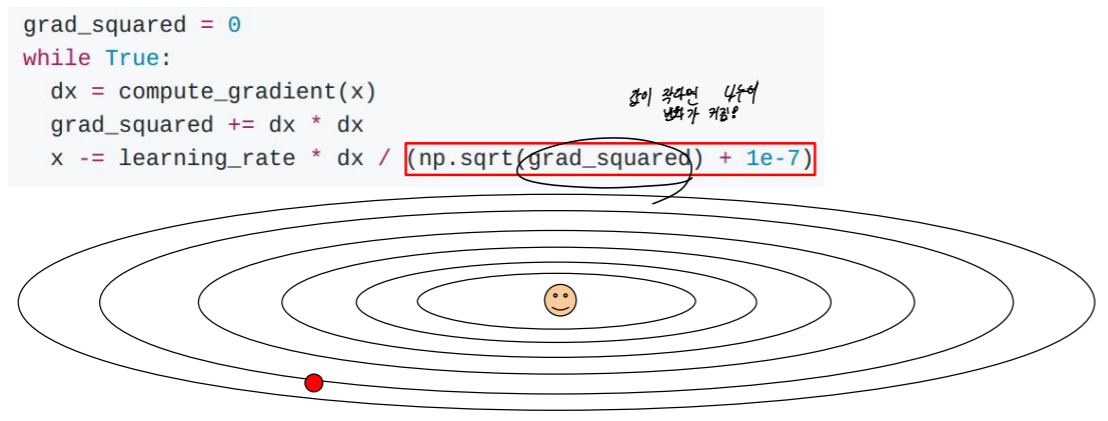
1e-7을 더해주는 이유는 grad_squared의 루트값이 0일 확률이 있기 때문에 구현상 저렇게 사용해준 것이다. 이렇게 함으로써 지금까지 지나온 모든 gradeint를 이용하여 optimize하는 것이 이 AdaGrad방식이다. 하지만 이 optimize방식에도 문제가 있다. optimize할 때마다 grad_squared의 값이 계속 커지게 되고, 이렇게 되면 x의 변화는 줄지만, grad_squared값은 계속 커지게 된다. 그렇다면 결국 어떤 점에서든 optimize되지 못하고, x의 변화량이 0에 수렴하게 되는 문제가 발생하게 된다. 이 문제를 해결하기 위해 grad_squared를 업데이트 할 때 grad_squared를 일정 비율 버리고, 현재 점에서의 gradient를 일정 비율 더하여 grad_squared가 너무 커지지 않으면서 모든 점의 gradient를 대변할 수 있게 된다. 특히, 이전 점에 대한 gradient일 수록 그 영향력은 줄어들 것이고, 현재 점에 가까울수록 그 영향은 커질 굿이다. 이 방식이 RMSProp이다.
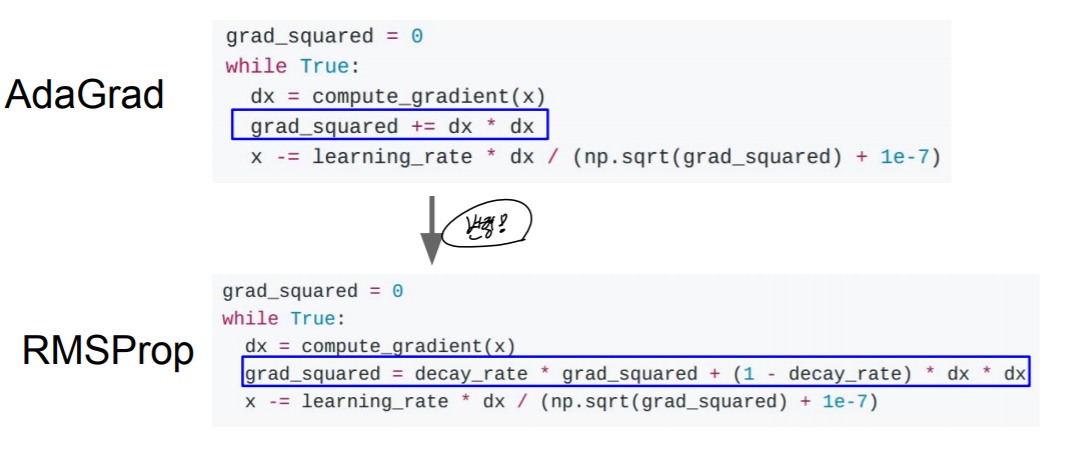
이제 지금까지 나왔던 optimize방식에 대한 경향성을 확인해보자.

AdaGrad는 변화량이 0이되며 사라졌고, SGD + Momentum은 급격하게 shoot over하지만 RMSProp은 미리 gradient를 조정함을 확인할 수 있다. 이에 따라 optimize속도가 더 빠르고, local optima에 빠질 확률이 줄어들게 된다.
5. Adam
Adam은 RMSProp방식과 Momentum 방식을 합친 방식이라고 생각하면 된다. 직관적으로 Adaptive gradient와 momentum를 함께 이용하고 싶다는 것이다.

하지만 이 방식에도 문제가 있는데 결국 모든 점에 대한 gradient를 나누는 방식때문이다. 첫 step에서는 grad_squared가 0이므로, 1e-7으로만 나누게 되는데 결국 첫 점에 대한 update가 너무 커지게 된다. 문제는 이 update가 optimize한 방향을 지나치고, 잘못된 local optima의 방향에 접근한다던가, 총 optimize 시간이 느려진다는 문제가 생긴다. 이 문제를 해결하기 위해서 bias를 추가해준다.
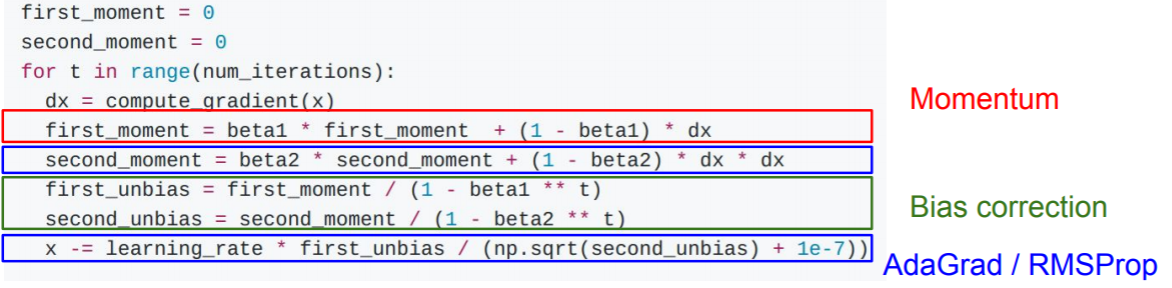
step수인 t를 추가함으로써 moment값들의 크기를 step을 고려하여 변경해준다 (step이 높을 수록 더 크게 나눈다)
실제 상황에서 Adam을 사용하는 것이 가장 좋으며 사용할 때 beta1 = 0.9, beta2 = 0.999, learning_rate = 1e-3 or 5e-4가 많은 모델들에 대한 좋은 시작점이라고 한다. 이에 대한 경향성을 함께 살펴보자.

지금까지 optimization방식들에 대해서 알아봤다. Loss에 대한 기울기를 이용하여 Loss를 최소화 한다는 의미는 같았지만, 어떤 gradient를 어떻게 사용할지에 대해서 방식들이 나뉘었고, 이에 따라 optimize 경향성도 눈에 띄게 차이남을 알게 되었다.
6. Reference
cs231n lecture 7
A Visual Explanation of Gradient Descent Methods (Momentum, AdaGrad, RMSProp, Adam)
Why can AdaGrad escape saddle point? Why is Adam usually better? In a race down different terrains, which will win?
towardsdatascience.com
'ML' 카테고리의 다른 글
| CNN 구조 (0) | 2021.07.06 |
|---|---|
| 인공지능 Learning rate, Regularization, Weight update, Transfer Learning (0) | 2021.07.05 |
| 인공 신경망 학습 (0) | 2021.07.05 |
| 합성곱 신경망 (0) | 2021.07.01 |
| 역전파와 신경 네트워크 (0) | 2021.07.01 |
