1. 목표
Spatial domain processing의 개념을 이해하고, transform domain processing과의 차이점에 대해서 알아본다
intensity transformation에 대해 알아본다.image histogram의 물리학적 의미를 이해하고 이를 이용해서 image enhancement를 한다.Spatial filtering의 메커니즘을 이해하고, 어떻게 적용할지 알아본다.
2. Background
앞선 목표에서도 보았듯이 이번 챕터의 목표는 Spatial domain에서의 연산을 이해하는 것이다. Spatial domain이라고 하면 뭔가 싶겠지만 간단하게 image plane 그 자체를 의미한다. 그리고 그 image plane(즉, 이미지 내의 픽셀 단위)에서의 연산이 이번 챕터에서 배울 것이다. 이러한 이미지의 픽셀을 직접 조작하는 연산을 image processing method라고 부른다. (transform domain에서의 image processing도 있고 frequency domain도 있지만 우선 이 챕터에선 이미지 픽셀으로 한정하고 이해하자)
이러한 Spatial domain에서 image processing을 다음과 같이 표현한다

f(x,y)는 input image를, g(x,y)는 output image를, T는 (x,y)와 주위 픽셀을 입력으로 하는 연산을 의미한다. 여기서 특수하게 단일 픽셀 연산이라면 이 연산을 intensity(gray-level, mapping) transformation function이라고 부르고 다음과 같이 표현한다.

그래서 이러한 연산으로 무엇을 할 수 있느냐? 라고 궁금할 수 있다. 다음은 그 예시이다.

위의 예시처럼 픽셀의 값을 직접 만짐으로서 이미지의 해석을 도울 수 있다. 이처럼 이미지를 조작하여 결과를 특정 application에 더 적합하게 만드는 것을 Enhancement라고 한다. 이러한 enhancement는 일반적으로 모든 application에 사용되는게 아니라, 특정 application에만 사용되는 problem-oriented한 성질을 갖는다.
이제 어떠한 Intensity transformation이 존재하는지 간단한 것 부터 차례대로 알아보자
3. Basic intensity transformation
가장 기초적인 Intensity transformation부터 알아보자.

위 transformation은 하나의 식으로 표현할 수 있는 단순한 transformation들이다. 각 transformation이 어떠한 경향성을 갖는지 그래프를 보고 확인하면서, 왜 이것을 사용하고 어디에 사용될 수 있는지에 대해서 알아보고자 한다.
3-1. Image negative
첫번째로 알아볼 transformation은 Negative이다. 그래프를 보면 알 수 있듯이, 단순하게 intensity를 뒤집는(reverse)연산이다. 다음은 그 식이다.

단순히 뒤집기만 하는데 뭐하러 이걸 사용하지? 라는 의문이 들 수 있는데, 다음 사진을 보면 이해가 쉽다

검정색이 지배적인 이미지에서 흰색을 찾는 문제가 주어졌을 때, 이를 그대로 보는 것 보다 negative를 적용하여 다음과 같이 반전하여 보는 것이 문제 해결에 더 좋다.
3-2. Log transformation
두번째로 알아볼 transformation은 Log transformation이다. Log 그래프를 보면 낮은 intensity로 변하는 input intensity는 매우 좁게 분포되어 있고 높은 intensity로 변하는 input intensity는 매우 넓게 분포되어있음을 확인할 수 있다. 즉, 이 연산을 적용하면 어두운(낮은 intensity) 픽셀들을 더 넓게, 구분되게, 밝게 할 것이고(Spreading), 밝은(높은 intensity) 픽셀들을 더 비슷하게 압축할 것이다.(Compressing) 이를 식과 예시를 보며 이해해보자.


이 변환에서 가장 중요한 것은 log의 식을 생각해보면 알 수 있듯이 픽셀 값의 큰 dynamic range를 압축한다는 것에 있다. Fourier spectur에서 이러한 특성을 더 쉽게 알아볼 수 있는데 이러한 스펙트럼은 매우 큰 값에 분포되어 있기 때문에 실제 디스플레이 시 선형으로 그대로 8bit color system으로 가져오면(if values are scaled lineary) 디테일이 뭉개질 수 있다. 이에 디테일을 살리기 위해, log로 낮은 intensity를 갖는 부분을 넓히고, 높은 intensity를 갖는 부분을 압축하여 오른쪽 사진과 같이 디테일을 살릴 수 있다.
3-3. Power-Law (Gamma) Transformaiton
다음은 지수함수이다. 루트까지 포함될 수 있다. 가끔 input intensity에 일정 offset을 넣어 표현하는 곳도 많으나 디스플레이 보정(display calibration) 과정에 문제가 되므로 생략하여 표현하는게 일반적이라고 한다. 지수함수의 경우 다음과 같이 표현된다.
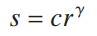
밑이 input intensity를, 감마가 주어진 상수이다. 감마의 크기가 1을 기준으로 낮다면 log와 마찬가지로 낮은 input intensity를 넓은 output intensity로 넓히고, 높은 input intensity를 좁은 output intensity로 압축하는 효과를 갖는다. 만약 1보다 크다면 반대의 효과를 가져올 것이고 1이라면 input과 output이 동일한 linear transformation을 처리할 것이다(모두 c가 1이라는 가정 하에) 이는 아래 그래프를 보면 더 쉽게 이해할 수 있을것이다.

위에서 서술한 내용을 그래프를 보며 쉽게 이해할 수 있다. 다음은 이에 대한 적용인 gamma correction(gamma encoding)의 예시이다. Cathod Ray Tube(CRT) Device에서 gamma값이 1.8~2.5인 지수함수로 표현되는 intensity-to-voltage 반응이 있는데, 이러한 반응때문에 모니터의 많은 부분이 검게 나타난다. gamma가 2.5인 위의 그래프를 보면 알 수 있듯이 많은 영역의 input intensity가 낮은 output intensity(어두운)로 mapping됨을 확인할 수 있다. 그렇기 때문에 이에 대한 역수(1/2.5 = 0.4)만큼 Gamma correction을 해주면 원본 이미지를 출력할 수 있다.

Power-law transformation의 다른 활용도 알아보자. 지수함수를 이용하면 손쉽게 general-perpose contrast manipulation이 가능해진다. 아까 log에서의 낮은 intensity의 디테일 살리기처럼 대비값을 조작하여 어둡게 표현된 부분의 대비를 높임으로서 패턴을 쉽게 확인할 수 있게 된다. 하지만 이에 대한 대비를 너무 높인다면 (즉 gamma값을 너무 낮추면) washed-out되어 악영향을 미칠 수 있다.

또한 log와 반대로 밝은 부분의 대비를 더 명확하게 하고 싶다면 gamma값을 일정 늘림으로서 높은 input intensity를 넓은 output intensity로 표현하여 디테일을 살릴 수 있다.

3-4. Piecewise linear transformation function
이는 다양한 linear function을 이어붙여 원하는 효과를 나타내는 방식이다. 다음 예시를 살펴보자.

이제 이 그래프를 보면 (r1, s1)부터 (r2, s2)까지의 대비가 증가하고, 나머지 영역의 대비가 낮아질 것임을 생각할 수 있다. 예를 들어 애매하게 어둡던 색이 확 어두워 질 것이고, 비슷해보이던 중간 intensity들이 명확히 구분하는 contrast stretching효과를 가져올 것이다.
두번째 예로 아래 그래프를 보자

이는 일정 threshold를 기준으로 넘으면 밝게, 넘지 못하면 어둡게 표현하여 흑백의 이미지를 도출할 것이다.
다음은 본 예시들의 결과이다.

위의 예시 말고도 linear function을 잘 배치한다면 contrast외에도 의도한 결과를 도출할 수 있을것이다. 만약 특정 이미지에서 추출하고자하는 패턴의 Intensity를 안다면 그 부분을 추출할 수도, 강조할 수도 있다. 이처럼 Intensity를 level별로 자르고 강조하는 것을 Intensity-Level slicing이라고 한다. 다음은 그 예시이다.
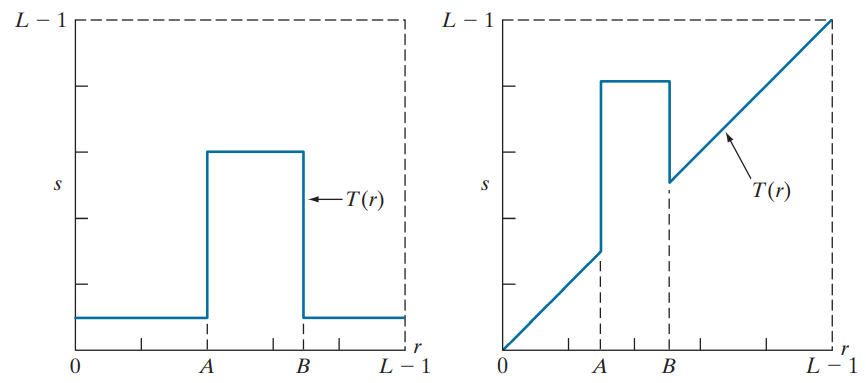

3-5. Bit-Plane slicing
이 이론은 Intensity를 Bit로 나타낼 때, 높은 Intensity가 많은 정보를 포함하고, 낮은 Intensity엔 노이즈가 포함된다는 아이디어에서 출발한 것이다.

이미지에 각 bit plane을 뽑아내면 다음과 같다.

이를 이용해, 이미지의 높은 bit만 잘라서 이미지를 축약하여 공간을 세이브하고 사용할때 reconstruction한다는 개념이다. 다음은 그 결과이다.

꽤나 눈으로 봤을때 구분이 불가능할정도로 잘 압축됨을 확인할 수 있다.
