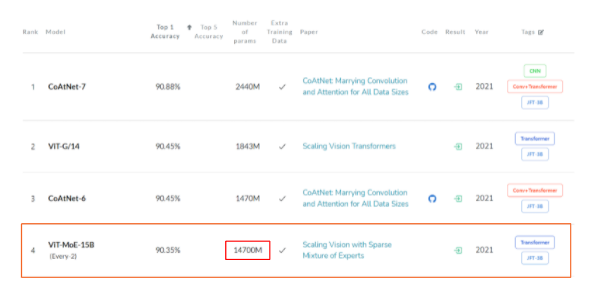
0. Scaling vision with sparse mixture of experts
본 논문은 Vision transformer를 개선시킨 논문이다. 이 논문의 키워드는 ViT의 Encoder 내 MLP(Multi Layer Perceptron)에 Conditional computation을 추가하였다는 것이다. (시간상 ViT 논문 리뷰는 생략)

여기서 Conditional computation이란 무엇일까? 일반 vision model들은 모두 dense하다. 즉, 입력에 대해 출력을 낼 때 모든 파라미터를 사용한다. 그런데 Conditional compuation은 모델을 sparse하게 만들자는 것이다. 즉, 입력에 대해 일정 condition에 부합하는 파라미터만 사용하고 모든 파라미터를 사용하지 말자는 것이다. 여기서 일정 condition으로 유도된 파라미터들은 그 condition을 매우 잘 해결하는 파라미터들일 것이다. 이 개념을 그림으로 보면 다음과 같다.

이와 같은 형태로 추론이 가능하다면 효율적으로, 많은 파라미터를 학습시킬 수 있을 것이다. 여기서 Conditional computation으로 Sparse한 모델을 구현한다는 장점이 나오는데, Model의 전체 파라미터는 매우 많지만, 추론에는 일부의 파라미터만 사용되므로 잘 학습된다면 성능은 낮아지지 않으면서 추론 속도는 매우 짧아진다.

이제 이를 구현하려면 네트워크는 어떤것을 학습시켜야할까? 어떠한 task를 task를 잘 푸는 전문가로 배정해주는 전문가 연락처(Gate)와 전달받은 task를 잘 해결해주는 전문가(Expert)를 학습해야한다.
여기서 입력은 ViT와 같이 Patch의 Embedding이고, 네트워크는 각 Embedding에 대한 Classification task를 풀 것이다.
1. Expert's Buffer Capacity
이제 목표를 알았으니, 어떻게 이를 학습할지에 대해 알아보자. 우선 Gate를 Balance하게 배정해야 할 것이다. 이를 위해 Expert의 갯수와 Expert의 Buffer의 크기를 고정해야 한다. 우선 Expert의 수에 대해서 생각해보자. 만약 Expert가 1과 비슷할정도로 작다면? Dense와 유사할 정도로 Statistical inefficiency를 가질것이고, 불공평한 Task배정은 HW Utilization을 악화시켜 Computational inefficiency를 야기할 것이다.
그리고 Capacity에 대해 알아보자. 논문에서는 다음과 같이 고정한다.

Capacity ration를 조정하여 각 Expert가 적절한 갯수의 패치를 담당할 것이다. 그런데 본 논문에서는 이 Capacity를 고의로 부족하게 한다. 즉, 각 Expert가 담당하는 patch의 수를 고의로 줄여서 모든 patch가 연산되지 않게한다. 즉, 손실되는 데이터가 존재한다는 의미이다.
왜 이렇게 하는것일까? 다음 그림을 보자

의미 없는 패치가 분명히 존재할 것이고, 이 패치는 연산량만 증가시키므로 패치의 중요도에 따라 필요하지 않은 패치의 연산을 고의로 피하고자 하는 것이다. 패치를 생략하는 이유와 근거를 알겠다, 그럼 이 중요도를 어떻게 판단할까? 각 패치에 대해 추론을 해서 가중치를 뽑는다면, 모든 패치가 적어도 1번, 많으면 2번씩 추론되므로 속도는 절대 빨라지지 않을것이다. 그렇기 때문에 각 Expert가 도출할 output을 기준으로 정렬하지 않고, 근사값을 이용해서 정렬한다.
본 논문이 제시하는 바는 바로 g(x) 즉, gate의 출력값이다. 이 출력값은 이전에 하나의 patch에 대해 각 expert가 얼마나 관련성이 있는지를 추론하여 patch를 높은 관련성을 도출한 expert에게 전달하여 conditional computation을 진행하기 위한 값이었다. Expert가 어떠한 task에 대해 optimize되었다고 할 때, 그 expert와 patch의 연관성이 높다면, 그 patch는 expert에서 높은 추론값을 도출할 것이라는 직관에서 부터 출발하여 이를 논한것이다. 그리고 이는 실험적으로 옳음을 확인하였고, 그래프를 통해 증명하였다. 다음은 그 예시이다.

이를 흐름 그래프로 나타내면 다음과 같다.

2. 학습
이제 개념을 다 알았다. g(x)로 task별로 expert에게 전달하고 각 expert는 전달된 task를 optimize한다. 그럼 이 학습은 어떻게 해야할까? expert의 학습은 g(x)를 통해 동일한 task별로 적절히 분배된다면 자동으로 학습될 것이다. 그렇다면 가장 중요한 g(x)는 어떻게 학습할까?
안타깝게도 본 논문은 task별로 expert에 어떻게 분배할지에 대해서 제시하지 못하였다. 다만, 각 expert에게 patch들을 밸런스있게 분배하는 방법에 대해서 제시하였고, 단순히 밸런스 있는 분배자 g(x)를 학습하면 task별로 expert에게 분배하는 분배자 g(x)와 근사할 수도 있다는 직관을 제시하였고, 그에 대한 실험적 결과를 제공하였다. "학습된 expert들의 weight를 가시화하고, 그것과 다른 학습된 네트워크의 경향성을 비교하여 task별로 expert에게 잘 분배하는 g(x)를 학습시켰다"라는 논리들이다.

사실 이 부분은 명확하지 않다고 느꼈다. 아마 논문도 그를 인지해서인지 g(x)의 학습의 정당성에 대해 명확히 말하지 못한 것 같다.
쨋든 그럼 논문이 주장하는 바가 맞다고 치고, g(x)를 어떻게 밸런스있게 학습할까? 올바른 학습 흐름을 위해 auxiliary loss를 이용한다고 한다. (auxiliary loss? 올바른 학습 흐름을 위해 맨 위에서만 Loss를 흘리는게 아니라 중간중간 흘리는 구조)
g(x)를 학습시키는 loss를 두가지로 나누자면, 1) patch와 expert의 연관성 학습 과 2) balanced routing이다. 이에 대한 수식은 아직 이해하지 못하였으니, 그저 내용을 정리하고 이해를 미루고자 한다

3. 결론
Conditional computation으로 엄청나게 많은 파라미터를, 추론 시간의 저하 없이 완성한 논문이다. 꽤나 높은 성능을 보였지만, 효율적으로 g(x)를 학습시킬지에 대해서는 조금 더 고민이 필요해보인다. 그리고 이에 대한 당위성 또한 고민해볼만한 부분인 것 같다.