1. 목표와 키포인트
1-1. 핵심
intensity의 discontinuity와 similarity가 핵심이다. Edge처럼 급변하는 Intensity를 기준으로 이미지의 Partition을 나눈다던가, 일정 기준으로 비슷한 partition을 나누는게 목표이다. 추가로 이 두개를 섞어 성능향상하는 내용, clustering과 superpixel을 통한 segmentation, graph cuts / pinciple region등을 알아본다
이를 통해 다양한 edge들의 특징을 이해하고, edge detection 방식에 대해 배우며(spatail filter와 그외 방법) 더 나아가 segmentation에 대해 배워본다.
2. 기초
2-1. Segmentation와 미분
intensity의 local discontinuities로 boundary를 찾는 Edge-based segmentation(a,b,c)이나 이미지를 여러 region으로 나누고, 일정 기준으로 유사성을 통해 boundary를 찾는 Region-based(d,e,f)이 있다

edge-based는 앞서 많이 봤으니 넘어가고, Region based의 경우 d처럼 texture로 인해 edge가 너무 많아 boundary를 찾는 척도로 사용하기 어려울 때 사용하는 듯 하다. 하지만 바깥의 intensity가 일정하다는 점을 바탕으로 region으로 나누고 region의 std=0이라면 바깥으로, 그렇지 않다면 안으로 판단하여 segmentation한다. 하지만 region으로 나누고 std를 구하여 region단위로 segmentation하다보니 boundary가 울퉁불퉁함을 확인할 수 있다.
2-2. Discrete domain에서의 미분 정의
미분이란 연속된 도메인에서 변화량을 나타내는 방식이다. 하지만 이미지는 연속되지 않은 이산 도메인이기 때문에 이에 대해 정의를 해주어야 한다. 이를 어떻게 정의하는가에 따라서 미분의 성격이 달라진다. 이미지에서는 주로 아래에서 서술할 central difference로 미분을 근사한다
2-2-1. central differences
central differences가 더 적은 오류를 도출하므로, 이를 사용한다. 이에 대한 정의는 다음과 같다.


미분을 위해 빼는 두 값이 중심점에 대하여 대칭적이라는 것이 특징이고, 이러한 특징으로 인해, 다른 미분 근사에 비해 더 적은 오류를 내포하는 것이다.
2-3. 이미지 패턴별 미분의 특성
그럼 이 미분을 이미지에서 어떻게 사용할까? 미분은 해당 점에서의 변화량을 나타내므로, 물체를 구분하는 edge를 추출하는 등에 사용될 수 있다. 우선 미분에는 어떠한 패턴이 있고, 각 패턴이 어떻게 이미지에 나타나는지 등을 알아보자, 아래 사진은 미분의 패턴과 이미지이다.

우선 값의 크기만 보면 2차 미분이 1차 미분에 비해 이미지 변화에 대한 민감도가 큼을 알 수 있다. 이를 근거로, noise, edge등을 얻기 위해 2차 미분을 이용할 수 있다.
미분이 이미지에 어떻게 나타나는지 특성을 보며 이해해보자
(1) 1차 미분은 두꺼운 edge를 만든다. .
(2) 2차 미분은 정밀한 디테일(라인, 노이즈 등)에 강하게 반응한다.
(3) 2차 미분은 ramp나 step에서 double edge반응을 도출한다.
(4) 2차 미분의 부호로 밝기의 변화를 유추할 수 있다.
2-4. 미분을 이용한 isolated point 검출 (Laplacian kernel)
이제 이 미분을 실제로 활용하여 이미지에서 특징을 추출해보자. 이번에 확인할 것은 isolated point이다. isolated point가 주위에 비해 튀는 값을 가지고 있다는 특징을 이용하여, 아래와 같이 정의된 필터를 이용하면 그 점을 얻을 수 있을것이다.


이 커널은 "Laplacian kernel"으로, 2차 미분의 근사 커널이다. (2차 미분이므로 double edge를 잘 처리해야할 것이다.) 이 라플라시안 커널은 isotropic하므로, 반응이 방향에 대해 독립적이라는 특징을 갖는다. (커널이 2D에서, X,Y,대각으로 정의되었으므로 이런 정의된 방향에만 독립)
아래는 그 예시이다. 대칭임에도 같은 반응을 보이는 것을 보면 이 커널이 방향에 독립적이라는 의미를 쉽게 이해할 수 있다.

2-5. 방향성을 갖는(unistropic한) 미분 방법
라플라시안과 다르게 방향성을 갖는 미분 방법이 있고, 문제에 따라 이러한 커널을 필요로 한다.(예시 : 한쪽 방향의 대각만을 추출하고 싶다면?) 아래는 그러한 커널의 예시와 적용의 결과이다.


3. EDGE MODELS(Step, Ram, Root edge)
3-1. Step, Ram, Root edge의 모습과 Intensity 그래프

3-2. Step의 특징
step edge는 명백히 다른 다른 레벨의 intensity로의 변화를 나타내는 패턴이다. (너무 뚜렷하다 보니, 고의로 스무딩을 먹여 리얼하게 보이는 경우도 있다). 이러한 step-edge model은 이후 설명할 Canny edge detection algorithm의 기초를 이루는 것 처럼 특징점 추출을 위해 사용될 수 있다.
3-3. Ramp의 특징( + 위의 Step특징에도 불구하고 ramp를 사용하는 이유)
위 step의 설명을 보면 step만 사용하면 될 것 같지만, 실제로는 그렇지 않다. 실제 디지털 이미지의 edge는 blur되어 있거나, noise가 낀 경우가 대부분이다. 따라서 두번째 이미지와 같은 스무딩된 edge 패턴을 이해해야할 필요가 있다. ramp에서는 단일 edge point는 존재하지 않게 되고, ramp 구간 내의 모든 point가 edge로 표현될 수 있다.
3-4. Roof Edge의 특징
Roof edge는 매우 얇고 sharpen된 edge에 대한 패턴이다.
3-5. 위 Edge model에 대한 예시

3-6. 미분의 특징과 결론
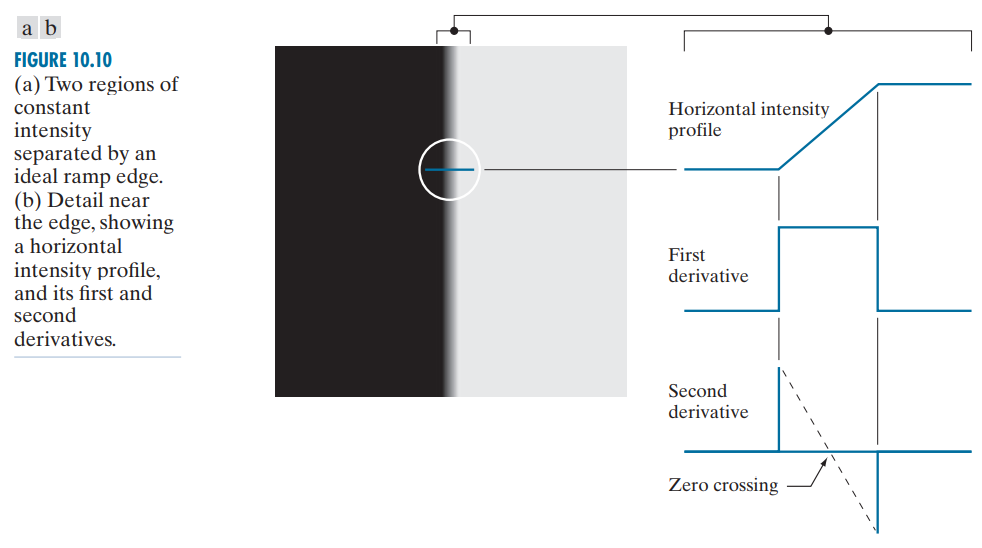
위와 같은 모델들과 예시들로 우리는 1차 미분의 크기로 edge의 존재 여부를 알 수 있었다.
3-7. Edge model과 미분에 대한 noise의 영향
실제 이미지는 Noise가 낄 수 있다. 따라서 노이즈가 낀 edge에 대하여 미분이 어떻게 나타나는지 다양한 edge model과 노이즈를 보면서 이해해보자.

이 예시는 미분이 노이즈에 매우 민감함을 보여주는 예시이다. 눈에 잘 띄지 않는 노이즈임에도 불구하고, 미분을 사용하기 어렵게 됨을 확인할 수 있다. 따라서 이러한 영향을 줄이기 위해 미분 이전에 smoothing하는 등의 기법이 주로 사용된다고 한다.
3-8. Edge detection과정
1. Image smoothing for noise reduction.
2. Detection of edge points.
3. Edge localization. (select from the candidate points only the points that are members of the set of points comprising an edge)
4. BASIC EDGE DETECTION
이제 미분을 이용하여 edge를 어떻게 찾고, 정의할에 대해 알아보자.
4-1. Gradient vector의 방향과 Edge의 방향
edge의 방향은 gradient와 직교하는 방향이다. 따라서 미분을 다음과 같이 정의할 때

이를 기반으로 edge의 방향을 다음과 같이 구할 수 있다.
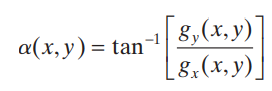
이 과정을 다음 예시를 통해 확인할 수 있다.


4-2. Gradient Operators
edge를 얻기 위해서는 우선적으로 gradient를 구해야 한다. 가장 먼저 알아볼 방법은 spatial kernel을 이용하여 얻는 방법이다. 각 커널마다 미분의 정의가 다르므로 특성도 달라 추출하는 edge와 noise도 달라진다.

가장 중심으로 인지해두어야 할 것은, prewitt와 달리 sobel이 중심 coefficient에 2를 배치함으로서 image smoothing효과를 도출하므로 noise reduction이나 edge검출에 더 효율적이라는 것이다. 각 필터에 대한 자세한 설명은 아래에 상세히 잘 나와있다.
https://blog.daum.net/trts1004/12109067
다양한 Edge(에지) 추출 알고리즘 : 1차미분, sobel, Prewitt, Roberts, Compass, Laplacian...
<에지 추출><?XML:NAMESPACE PREFIX = O /> 1. 에지 개념 1) 정의 - 가장 자리라는 의미 - 또는 윤곽선이라 함 - 영상의 밝기가 낮은 값에서 높은 값으로, 또는 그..
blog.daum.net
4-3. Gradient의 방향과 크기
미분 크기를 정의하면 일반적으로 다음과 같이 정의된다
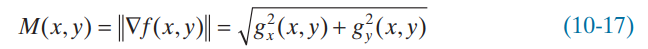
하지만 이 방식에는 제곱과 제곱근 연산을 사용해야하므로, 연산량이 높아져 속도에 악영향을 끼칠 수 있다. 따라서 크기를 단순하게 다음과 같이 근사하여 표현할 수 있다.

이러한 근사는 intensity크기를 이전과 같이 표현할 수 있으면서 연산량을 줄일 수 있다는 장점이 있지만, 그에 대한 대가로 필터가 istropic해진다는 문제가 생긴다. (x,y축 모두에서 x에 대한 미분과 y에 대한 미분을 뽑거나, x에 대한 미분을 뽑을 땐 x에 대해서만, y에 대한 미분을 뽑을 땐 y에 대해서만 사용하는 방향으로 근사하기 때문에)
그런데 이 방식은 Prewitt and Sobel이 어차피 vertical, horizontal edges에 대해서만 isotropic하므로 상관이 없다
원문 : This equation is more attractive computationally, and it still preserves relative changes in intensity levels. The price paid for this advantage is that the resulting filters will not be isotropic (invariant to rotation) in general. However, this is not an issue when kernels such as the Prewitt and Sobel kernels are used to compute gx and gy because these kernels give isotropic results only for vertical and horizontal edges. This means that results would be isotropic only for edges in those two directions anyway, regardless of which of the two equations is used.
4-4. Angle에 따른 미분을 구하는 Kirsch compass kernels

문제에 따라서 특정 방향에 대해서만 edge를 뽑아야 할 필요성이 존재한다. 따라서 이를 위한 커널이 필요하다. 수평, 수직 sobel이 대각선에 민감하긴 하나, 대각에 대해 미분 가능하진 않기 때문에 필요성이 있다. 아래 그림이 그 필요성에 대한 예시이다.

하지만 이러한 경우에 kirsch compass kernel을 먹이면,
아래와 같이 원하는 edge를 추출할 수 있다.

4-5. Gradient와 Trhesholding
Gradient의 크기를 바탕으로 뚜렷한 특징(edge)만 필터링 할 수 있다.

이처럼 smoothing 뿐만 아니라, thresholding도 효과적인 edge detection에 활용할 수 있다.
