1. 소개
Sharpening은 intensity를 강조하여 medical image이나 electronic printing 등에서 패턴인식을 위한 image enhancement를 위해 사용된다. Lowpass때는 integration을 통한 Averaging이였다면, 여기서는 Differentiation을 통한 Intensity 변화량 강조이다. 즉, 점에서의 미분값이 Intensity 불연속성(노이즈와 같은 튀는 값)과 비례할 것이기때문에, image differentiation은 edge / 노이즈와 같은 불연속성을 강조하고, 천천히 변화하는 지역을 억제할 것이다.
이를 lowpass때 처럼 Frequency domain에서 생각해보자면 sharpening은 highpass filtering으로 높은 frequencies만(Intensity가 급변하는 -> 예 : Edge) 넘기고 낮은 frequencies를 무시하는 형태를 띌 것이다
2. 기초
그럼 미분으로 sharpening을 수행할 수 있음을 알겠다. 그럼 어떻게 discrete한 spatial domain에서 미분을 할까?가 문제가 된다. 여기서는 이걸 어떻게 할지에 대해서 알아보고자 한다.
미분은 다음과 같은 특징을 띄어야 한다.
1. intensity가 동일한 지역에서는 0이어야 한다.
2. intensity가 변하기 시작하는 부분(즉 ramp와 step의 시작부분)에서는 0이 아니여야 한다.
3. intensity가 일정하게 변하는 부분(ramp)에서는 0이어야 한다.
이와 같이 2차 미분은 다음과 같은 특징을 가져야 한다.
1. intensity가 동일한 지역에서는 0이어야 한다.
2. intensity가 변하기 시작하는 부분(즉 ramp와 step의 시작과 끝)에서는 0이 아니여야 한다.
3. intensity가 일정하게 변하는 부분(ramp)에서는 0이 아니여야 한다.
input과 output의 discrete한 값 영역이 유한하게 제한되어 있으므로 미분값도 유한하게 일정 범위 내에 정의될 것이다.
미분의 정의에 의해 Discrete한 1D에서의 미분을 다음과 나타낼 수 있다.

이를 이용하여 2차 미분을 나타내면,

로 나타낼 수 있다.
Intensity변화 양상에 대한 1차 미분값과 2차 미분값의 변화 양상을 예시를 들어 살펴보자.
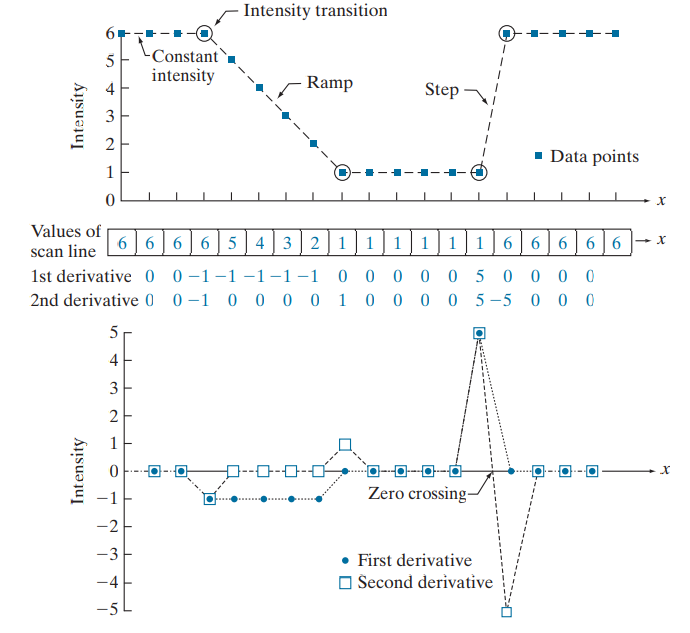
위는 각 상태들을 표현한 예시 및 그래프이다. 각 예시에 따라 1차 미분값과 2차 미분값을 계산하였고, 이를 그래프로 표현하였다.
Intensity가 변하지 않고 일정할 때(Constant intensity ) / Intensity transition으로 인해 Intensity에 불연속성이 생길 때 (step and ramp discontinuities) / 불연속 이후에 일정하게 Intensity가 변할 때 (Ramp) / 발생하는 불연속 성은 noise나 line이나 edge를 표현할 확률이 높다. 특히, 미분값이 양수에서 음수로 (혹은 반대)변할 때 즉, zero crossing에서 높은 확률로 만족한다. ramp에서도 미분값이 0이 아니므로 edge가 발생할 순 있는데, Intensity가 꾸준히 변하는, 두꺼운 edge일 것이다.

따라서 원하는 바가 물체를 명확히 구분하는 edge나 line이라면 2차 미분에서 0에 의해 나눠지는 2개의 edge(하나는 양수, 하나는 음수)를 찾으면 1차 미분보다 훨씬 더 명확한 edge를 찾을 수있을 것이다. 추가로 2차미분의 연산이 더 간단하다.
3. Second derivative을 통한 Image sharpening (Laplacian)
이제 edge 검출을 위해 Discrete한 2D공간에서의 2차 미분을 정의하고, 정의한 함수를 filter kernel로 만들고, 이를 연산하는 과정을 거쳐야 한다.
Lowpass filter인 Gaussian의 특징이었던 isotropic(동방향성, 출력과 방향간 입력분포의 독립성, 방향과 출력의 독립성)을 계승하여, isotropic한 미분 연산인 Laplacian을 다음과 같은 절차로 고안하였다.

일단 미분을 정의한다
라플라시안의 정의에 의해 x와 y의 편미분으로 표현하면,

그리고, Discrete한 2D Spatial domain에서의 미분을 다음과 같이 정의한다.

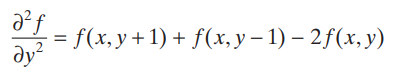
따라서,

와 같이 표현할 수 있다. 여기서 미분이 linear operation이므로, Laplacian또한 linear operation이다. 이를 convolution을 위한 filter kernel로 나타내면,
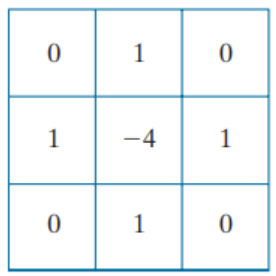
이다. 라플라시안에 대각방향을 추가한다면, f'(x+1, y+1) - f'(x-1, y-1) = f(x+1, y+1) + f(x-1, y-1) - 2 * f(x, y)이므로

와 같이 표현될 수 있다. 첫번째 커널은 90°의 rotation에 대해 isotropic하고, 두번째 커널은 45°의 rotation에 대해 isotropic함을 확인할 수 있다.
이 filter의 계수합은 0이므로, 미분 커널으로 constant region에 대해 연산할때 결과는 0일 것이고, 그 영역 전체가 일정할 것이다 그리고 원본 이미지와 filter를 거친 이미지의 픽셀값의 합이 같으므로, bias가 생기지 않을 것이다.
계수의 합이 0인 filter로 convolution연산 한다는 것은 결과의 합 또한 0이됨을 의미하는데 이는 픽셀에 음수값이 포함된다는 의미이고, 음수를 표현할 수 없으므로 이러한 픽셀의 처리를 위해 원본 이미지를 더해주는 등의 작업이 필요하다

이를 결과와 함께 살펴보자.

두번째 사진은 라플라시안 필터를 거친 이후, 음수를 0으로 변경한 후 출력한 이미지이다. 세번째는 원본 이미지에 선형 라플라시안 필터 결과값 * -1을 한 결과인데 디테일(intensity의 불연속성이 존재하는 부분의 contrast의 증가)이 더 살았음을 확인할 수있다.
마지막 사진은 선형 + 대각 라플라시안을 적용한 결과 -1을 곱하고 원본 이미지에 더한 결과이다. 대각 방향에 대한 미분을 추가하였기 때문에 디테일이 사는 것이다.
4. UNSHARP MASKING AND HIGHBOOST FILTERING
다른 sharpening 방법으로는 smoothing(unsharp) 한 결과를 이용하여 edge가 도드라지는 결과를 얻는 방법이다. 이는 다음 절차로 시행된다
1. 이미지를 블러한다
2. 오리지널 이미지에 블러한 이미지를 빼서 mask를 만든다.
3. 만든 mask를 k만큼 곱한 다음, 원본이미지에 더한다

이를 수식으로 나타내면,


이때 곱해지는 k의 범위에 따라 용도가 세분화 된다. 이는 다음과 같다
When k = 1 we have unsharp masking, as defined above.
When k > 1, the process is referred to as highboost filtering.
When k < 1, reduces the contribution of the unsharp mask
이러한 unsharp mask는 2차 미분을 한 결과와 유사하므로, 이를 시행하면 변화량이 급격한 포인트를 강조할 수 있다.
다음은 그 예시이다. 밑에 두 사진은 K의 변화에 따른 결과 변화인데, K가 커질 수록 더 강조가 되는 것은 맞으나, 너무 커진다면 mask의 음수값으로 인해 어두운 후광이 과해질 수 있다.

5. 1차 미분(Gradient)를 통한 Image sharpening
1차 미분으로 Image sharpening하는 방식이다. 픽셀 값의 변화량을 바탕으로 gradient를 다음과 같이 나타낼 수 있다.


gradient vector는 그의 원소들이 미분가능하므로, linear operation이다. 하지만 gradient의 크기는 root와 제곱으로 인해 nonlinear하다. 반면에 vector표현은 rotation invariant하지 않지만 magnitude는 rotation invariant하다. 어떠한 식에서는 Magnitude를 다음과 같이 표현하기도 한다.

이 식또한 intensity의 크기를 표현하긴 하지만 isotropic property를 읽게 된다는 문제가 있다. 하지만 미분의 근사형태인 라플라시안은 일정 각도에 대해 isotropic한 것 처럼 대부분의 미분 근사 kernel이 90°의 회전에 대해 isotropic하다는 특징을 가지므로, 두 식모두 사용에 문제가 없다.
이제 이걸 어떻게 kernel 형태로 나타낼지에 대해 고민해보자. 다음과 같은 형태의 kernel이 있다고 가정하자
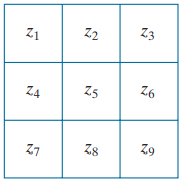
이때 자주 사용되는 근사 1차 미분 커널에는 1) 로버츠 마스크 와 2)소벨 마스크 가 존재한다. 먼저 로버츠 마스크를 살펴보면, 대각의 차를 이용해 x와 y의 gradient를 구하는 방식으로 다음과 같이 표현할 수 있다.

하지만 이는 짝수크기의 커널이므로, center of spatial symmetry를 만족하는 odd size의 kernel의 필요성이 대두되었다. 그래서, 소벨 마스크는


와 같이 x와 y의 gradient를 구한다. 이 또한 모든 계수항의 합은 0이고, 중앙에 2를 배치하여 중요도를 높게 배치하는 방식이 중요하다.
이렇게 gradient를 나타내고, magnitude를 얻는다.

로버츠는 왜 대각으로 gradient를 계산하지? 왜 소벨이 수직, 수평 마스크 연산만 하는데 어떻게 대각 엣지를 추출하지? 프리윗보다 수평 수직의 비중이 높은데 왜 소벨이 대각선 방향에 높인 엣지에 민감하게 반응하지? 라는 궁금증에 찾아봤다. 이러한 특징을 왜 갖는지는 이해하겠는데, 더 좋은 방법이 없는지는 궁금하다

